IndexFiguresTables |
Ji-hyun Lee , Hyung-in Ra , Ki-man Kim and Jeong-woo HanSymbol Timing Error Estimation Using Constellation Histogram and CNN in SOQPSK-TG ModulationAbstract: In this letter, we present a symbol timing error estimation method for SOQPSK-TG modulation, which is one of the partial response continuous phase modulation schemes and defined in the IRIG-106 international telemetry standard. In the proposed method, we apply the constellation histogram of the preamble and convolutional neural network (CNN). The performance of the proposed method for symbol timing error estimation is demonstrated via simulation results. Keywords: IRIG-106 Telemetry Standard , Partial Response Continuous Phase Modulation , Symbol Timing Error Estimation , SOQPSK-TG , CNN Ⅰ. 서 론원격 계측은 항공기 개발 단계에서의 테스트나 발사체 모니터링 등을 위해 수집된 정보를 무선 통신을 통해 전달한다. 이를 위해 IRIG(Inter-Range Instrumentation Group)-106이라는 국제 표준이 수립되어 있다[1,2]. 이 표준에는 데이터 전송을 위하여 SOQPSK-TG (shaped offset quadrature phase shift keying-telemetry group)라는 변조 방식이 다른 전송 방식들과 함께 포함되어 있는데 이는 이전 데이터와 상관성을 갖는 3항(ternary) 알파벳 심볼을 기반으로 하며, 연속적인 위상 변화가 있는 특징을 갖는다. 일반적인 디지털 전송 시스템의 수신기에서 최적의 복조를 달성하기 위해 심볼 타이밍 동기화는 중요한 과정 가운데 하나이다. 이 과정에는 심볼 타이밍 오차 추정을 포함하는데 프리앰블 기반의 동기화가 대부분을 이루고 있다. 기존의 대표적인 심볼 타이밍 오차 추정 방법으로써 미리 정해진 시간 간격으로 샘플링하여 타이밍 오류를 탐지하는 Early-late 방식, 두 개의 인접한 샘플을 사용하여 타이밍을 추정하는 Muller-and-Mulle 방식 및 신호의 영점 교차 지점을 사용하여 동기화하는 Gardner 방식 등이 많이 알려져 있다. 특히, Gardner 방식은 구조가 간단하면서도 미지의 반송파 위상에 대한 독립성을 갖추고 있는 장점을 갖고 있지만 도플러 천이나 지터가 큰 경우 클록 동기화 장치의 심볼이 삭제되는 끊김(hang-up) 문제를 유발할 수 있다[3]. 또한 OQPSK (offset quadrature phase shift keying) 변조를 위해 위상에 민감하지 않은 심볼 타이밍 추정기가 제안되었지만 많은 계산량을 필요로 하는 단점이 있다[4]. 최근 많은 응용 분야에서 딥러닝을 활용하는 사례들이 증가하고 있다. 심볼 동기화 타이밍 추정 분야에서도 1차원 파워 스펙트럼 이미지를 사용하여 CNN(convolutional neural network) 기법을 적용하는 방법이 제안되었다[5]. 이 방법은 높은 SNR (signal-to-noise ratio) 환경에서 좋은 결과를 보였지만 스펙트럼이 1차원 이미지이기 때문에 CNN 기법의 특징 추출 능력이 충분히 활용되지 않아 계산량에 비해 정확도가 낮은 문제를 보였으며, OFDM (orthogonal frequency division multiplexing) 전송을 위한 것이다. 이에 SOQPSK-TG 전송과 같은 연속 위상 방식의 특징을 이용한 심볼 타이밍 오차 추정 방법이 필요하다. 이 레터에서는 원격 계측 표준으로 정의된 SOQPSK-TG 신호의 수신부에서 누적 성상도와 CNN을 이용한 심볼 타이밍 오차 추정 방법을 제안하였다. 발사체 모니터링 환경과 같이 AWGN (additive white Gaussian noise) 채널로 근사되는 환경에서의 모의실험 결과를 제시한다. Ⅱ. 누적 성상도와 CNN을 이용한 심볼 타이밍 오차 추정SOQPSK-TG 변조는 부분 응답 연속 위상 변조 방법 가운데 하나이며, 다음의 식과 같은 기저대역 복소 신호 모델로써 표현된다.
식(1)에서 [TeX:] $$T_b$$는 한 심볼의 길이이며, h는 변조 지수로써 SOQPSK-TG에서는 0.5로 정의되어 있다. [TeX:] $$x_m$$은 {-1,0,+1} 가운데 하나의 값을 갖는 3항 심볼로써 프리코더의 출력이며, 이는 과거 데이터 값에 의해 영향을 받는다. 또한 식(1)에서 [TeX:] $$q_{T G}(t)$$는 위상 펄스라고 하며, 이는 IRIG-106 표준에 정의된 주파수 펄스를 적분한 것이다[1]. 제안하는 방법은 패킷의 일부인 프리앰블 구간의 누적 성상도 이미지를 사용한다. 그림 1(a)에는 IRIG-106 표준에 정의된 몇 가지 프리앰블 가운데 24-bit 길이의 값을 SOQPSK-TG 방식으로 변조하고, 심볼 당 샘플 수를 16개로 한 경우의 누적 성상도를 나타내었다. 이때 3항 심볼 생성을 위한 초기 값들은 모두 0으로 설정하였다. 여기서 누적 성상도는 프리앰블 구간에서 심볼 내의 샘플 단위에서 성상도를 표현하되 같은 값은 지속적으로 누적하여 나타낸 히스토그램을 의미한다. 그림 1(a)에 나타낸 누적 성상도는 심볼 타이밍 오차가 없는 경우로써 이를 위에서 내려다 본 것이 그림 1(b)이며, 그림 1(c)는 10 샘플의 심볼 타이밍 오차 발생을 가정한 경우이다. 이들은 (32×32) 픽셀을 갖는 이미지이며, 각 픽셀의 점들은 그레이 스케일을 사용하여 누적된 정도를 표현하였다. 그림으로부터 심볼 타이밍 오차가 발생하면 누적 성상도가 회전하는 형태로 변화하며, 이러한 변화의 정도인 회전각을 CNN을 이용하여 추정한다. 이 누적 성상도를 기준으로 수신된 프리앰블이 어느 정도 틀어졌는지 추정하여 심볼 타이밍 오차를 추정한다. 심볼 당 16 샘플을 가정하면 SOQPSK-TG 신호는 총 128개의 위상값이 가능하며, 학습에서 이를 기준으로 틀어진 회전각을 판단하였다. 그림(Fig.) 1. (a) 정확한 심볼 타이밍을 갖는 경우의 누적 성상도, (b) 정확한 심볼 타이밍의 누적 성상도를 위에서 본 모습, (c) 10 샘플 타이밍 오차가 있는 경우의 누적 성상도를 위에서 본 모습 ((a) Constellation histogram in case of accurate symbol timing, (b) Top view of Fig. 1(a), (c) Top view of constellation histogram with 10-sample symbol timing error) 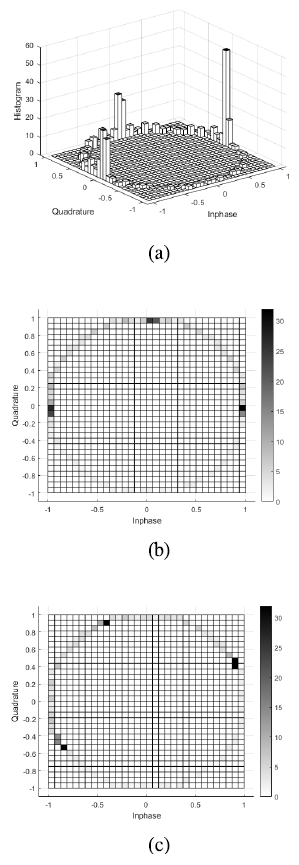 기준이 되는 누적 성상도와 심볼 타이밍 오차 발생으로 인하여 위상이 변화한 이미지 및 해당하는 회전각 정보를 입력하여 CNN으로 학습시킨 후, 검증을 위해 회전각을 알려주지 않고 임의의 위상 회전을 갖는 이미지만 입력하여 해당 이미지에 대한 각도를 추정하고, 이를 심볼 타이밍 오차로 변환하도록 하였다. Ⅲ. 모의실험 결과SOQPSK-TG 변조된 신호의 심볼 타이밍 오차 추정을 위해 제안한 누적 성상도를 이용한 알고리즘의 성능을 확인하기 위해 모의실험을 수행하였다. 모의실험에는 우선 표준에 정의된 24-bit 길이의 프리앰블을 사용하였고, 한 프레임 내에서 심볼 타이밍 변동은 없다고 가정하였다. 심볼 당 16개의 샘플로 구성되도록 하였기 때문에 프리앰블 구간은 총 416개의 샘플로 구성된다. 심볼 타이밍이 정확할 때의 프리앰블 샘플 위상점을 기준으로 수신된 신호의 심볼 타이밍 오차로 인한 위상 회전각을 CNN 알고리즘을 통해 학습하였다. 학습 과정의 입력으로는 1개 심볼 오차 내에 해당하는 ±15 샘플, 즉, 약-42.2도부터 약+42.2도에 해당하는 위상점 데이터의 그림과 각 그림에서 정답이 되는 위상점에서 틀어진 각도 정보를 입력하여 각 샘플마다 30개의 회전된 이미지와 1개의 정답 이미지를 입력으로 받아 정답으로부터 얼마나 회전되었는지를 학습하게 된다. 모의 실험은 GPU로써 NVIDIA GeForce GTX 970 모델이 장착되고, 윈도우 10을 사용하는 컴퓨터에서 MATLAB을 사용하여 수행되었다. 또한, 계산량을 감안하여 1 심볼 길이에 해당하는 회전 각도로 제한하여 진행하였다. 데이터의 다양성을 위해 각 회전된 이미지마다 0 dB부터 20 dB까지 0.4 dB 단위로 SNR을 조정하여, 정답의 이미지와 함께 입력으로 사용하여, 각 샘플마다 총 1,580개의 위상 왜곡된 이미지와 정답 이미지를 입력하여 학습하였다. 학습은 총 100회 반복하여 다양한 SNR 환경에서도 회전 각도를 추정할 수 있도록 하였다. 학습 입력 데이터의 크기가 (32×32)인 것을 고려하였을 때 최대 5층 깊이의 CNN 모델을 설계할 수 있는데 결과를 도출하기 위해 사용된 파라미터들을 Table 1에 나타내었다. 표(Table) 1. CNN을 위한 파라메타 (Parameters for CNN)
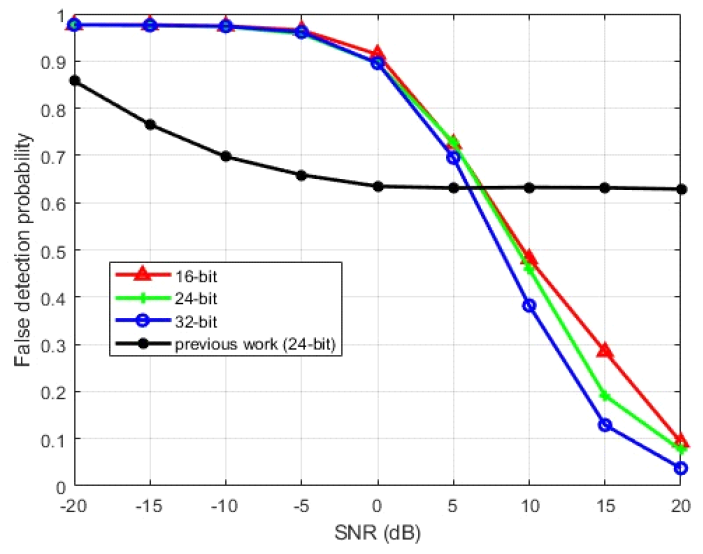
그림 2는 합성곱 층수에 따른 오답률을 나타낸 것으로써 검증을 위해 틀어진 각도는 학습 구간과 동일하게 설정하고, SNR을 -20 dB에서 20 dB까지 5 dB 단위로 무작위 입력하였을 때, 총 10,000회 반복 실행하여 도출된 것이다. 그림에서 CNN 모델 기반 데이터는 추정된 값이 정답과 1 샘플이라도 오차가 날 경우 오답으로 처리하였다. 또한 그림에는 기존의 방법[6]으로 처리한 결과도 함께 나타내었는데 대체로 SNR이 약 10 dB 이상인 경우에 제안한 방법이 낮은 오답률을 보여주었다. 그림(Fig.) 2. 합성곱 층수에 따른 오답률 (False detection probabilities according to the number of CNN convolutional layers) 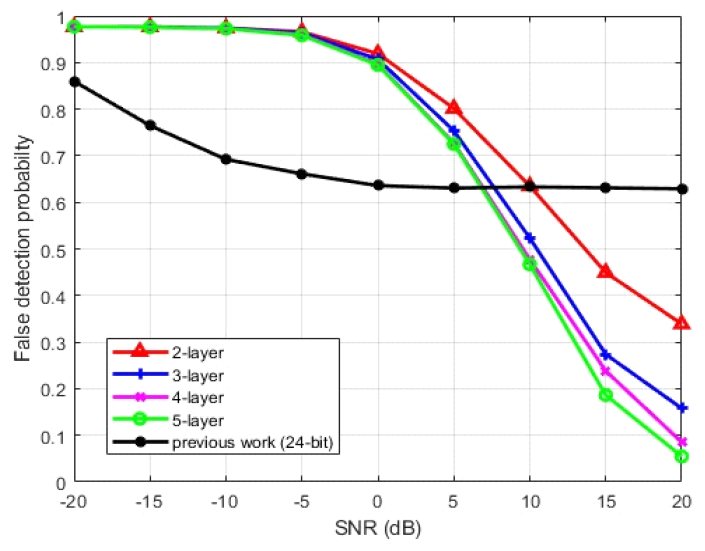 그림 3은 24-bit 길이의 프리앰블 이외에 IRIG-106 표준에서 동시에 제시된 16-bit와 32-bit 길이의 프리앰블 값을 같은 CNN 모델에 적용하여 추정된 오류율을 나타낸 것으로 프리앰블의 길이가 증가하면서 오답률이 조금씩 감소하는 형태를 보였다. 오답률 0.1을 기준으로 볼 때 32-bit 길이가 16-bit 길이보다 약 3 dB 정도의 차이를 보였다. References
|
StatisticsCite this articleIEEE StyleJ. Lee, H. Ra, K. Kim, J. Han, "Symbol Timing Error Estimation Using Constellation Histogram and CNN in SOQPSK-TG Modulation," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 10, pp. 1560-1563, 2025. DOI: 10.7840/kics.2025.50.10.1560.
ACM Style Ji-hyun Lee, Hyung-in Ra, Ki-man Kim, and Jeong-woo Han. 2025. Symbol Timing Error Estimation Using Constellation Histogram and CNN in SOQPSK-TG Modulation. The Journal of Korean Institute of Communications and Information Sciences, 50, 10, (2025), 1560-1563. DOI: 10.7840/kics.2025.50.10.1560.
KICS Style Ji-hyun Lee, Hyung-in Ra, Ki-man Kim, Jeong-woo Han, "Symbol Timing Error Estimation Using Constellation Histogram and CNN in SOQPSK-TG Modulation," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 10, pp. 1560-1563, 10. 2025. (https://doi.org/10.7840/kics.2025.50.10.1560)
|