Secrecy Performance and Diversity Order with Scheduling Schemes in LEO Satellite Networks

Ⅰ. 서 론

최근 무선 통신 시스템에서는 보안성에 대한 관심이 급격히 증가하고 있다. 특히, 위성 네트워크의 경우 넓은 서비스 범위와 높은 데이터 처리량으로 인해 안전한 통신 채널의 확보가 필수적인 과제로 떠오르고 있다^[1]. 통신 시스템에서 기존의 보안 방식은 주로 전통적인 암호화 기술을 활용하였으나, 위성의 하드웨어 제약으로 인해 새로운 형태의 보안 통신 방법 연구에 대한 필요성이 제기되고 있다. 물리계층보안(Physical Layer Security, PLS)은 무선 채널의 고유한 특성을 활용하여 물리계층 단에서 신호처리 기법으로 무선통신의 보안성을 높일 수 있는 연구분야로 각광을 받고 있다^[2]. 본 연구는 도청을 시도하는 공격자가 무인 항공기(Unmanned Aerial Vehicle, UAV)의 형태로 존재하는 상황에서 다수의 위성 중 데이터 전송에 적합한 위성을 선별하는 스케줄링 알고리즘의 보안 성능을 분석한다.

Ⅱ. 시스템 모델

본 연구에서는 단일 안테나를 갖춘 N개의 저궤도 (Low Earth Orbit, LEO) 군집위성, [TeX:] $$M_b$$개의 안테나를 갖춘 지상 기지국(Ground Base Station, GBS) 및 [TeX:] $$M_e$$개의 안테나를 갖춘 악의적인 무인 항공기(UAV)가 존재하는 상황을 가정한다. 악의적인 UAV의 목적은 위성에서 지상국으로 전송되는 신호를 도청하는 것이다. 위성 인덱스 [TeX:] $$n \in\{1, \ldots, N\}$$에 대해서 위성 n에서 GBS로의 채널 벡터를 [TeX:] $$h_n \in C^{M_b \times 1}$$로, 위성 n에서 UAV의 채널 벡터를 [TeX:] $$g_n \in C^{M_t \times 1}$$로 정의한다.

본 연구에서는 채널 벡터의 각 요소를 모양(shape) 매개변수 m과 척도(scale) 매개변수 Ω를 갖는 Nakagami-m 확률 변수로 모델링하고 독립 동일 분포(independent and identically distribution, i.i.d.)를 가정한다. Nakagami-m 채널 모델은 저궤도 위성 통신 관련 연구에서 많이 사용되고 있으며 위성 네트워크의 고속 이동성, 시야각 제약 등의 특징으로 인해 발생할 수 있는 무선 채널의 통계적 불확실성을 모델링할 수 있다^[3,4]. 예를 들어, Nakagami-m 채널 모델은 형상 매개변수 값과 척도 매개변수 값을 통해 위성과 지상국 사이의 가시성(LoS)과 비가시성(NLoS)의 영향을 조정할 수 있다.

GBS와 UAV는 최대비율결합(Maximum Ratio Combining, MRC) 수신기를 사용한다. GBS는 가장 높은 채널 이득을 가진 위성 [TeX:] $$n^*$$을 스케줄링 하며, 이 스케줄링 기법을 MRC-Max 기법으로 명명한다. 이때, GBS와 UAV의 수신 신호 대 잡음비(Signal-to-Noise Ratio, SNR)은 각각 다음과 같다:

여기서 [TeX:] $$\theta=\Omega / m, \rho_b \mid \doteq P_0 / \sigma_h^2, \rho_e \doteq P_0 / \sigma_g^2$$이며, [TeX:] $$P_0$$는 위성의 전송 전력, [TeX:] $$\sigma_h^2 \text { 와 } \sigma_g^2$$는 각각 GBS와 UAV에서의 평균 잡음 전력을 나타낸다. MRC-Max 기법은 선형 탐색으로 구현 가능하며 O(N) 복잡도를 가진다. 또한 MRC-Max 기법은 GBS의 채널 정보 ([TeX:] $$h_n$$)만을 이용하며 UAV의 채널 정보([TeX:] $$g_n$$)를 사용하지 않는다.

GBS와 UAV에서 각각 달성 가능한 전송 속도와 이를 바탕으로 계산되는 보안 전송률(secrecy rate)은 다음과 같다: [TeX:] $$r_s=\max \left\{r_b-r_e, 0\right\},$$ 여기서, [TeX:] $$r_b \text { 와 } r_e$$는 [TeX:] $$r_b=\log _2\left(1+\gamma_b^*\right) \text { 와 } r_e=\log _2\left(1+\gamma_e^*\right)$$을 의미한다.

최종적으로 [TeX:] $$R_0$$의 보안 전송률 요구사항을 가정했을 때, 보안 아웃티지 확률(SOP)은 다음과 같다.

추가적으로 [TeX:] $$R_0=0$$으로 설정할 경우, 보안 아웃티지 확률([TeX:] $$p_{s o}(0)=\operatorname{Pr}\left\{\gamma_b \lt \gamma_e\right\}$$)은 도청자 링크의 전송률인 [TeX:] $$r_e$$이 지상국 링크의 전송률인 [TeX:] $$r_b$$보다 큰 상황이 발생하는 확률을 의미하게 된다. 이는 가로채기 확률 (intercept probability)로 다음과 같이 정의된다.

Ⅲ. 보안 아웃티지 확률 분석

본 장에서는 위성 통신에서 MRC-Max 기법의 보안 아웃티지 확률과 다이버시티 차수를 분석한다.

3.1 보안 아웃티지 확률 분석

MRC-Max 스케줄링 기법을 사용했을 때, SNR [TeX:] $$\gamma_b^*$$의 누적분포함수(Cumulative Distribution Function, CDF)는 다음과 같다:

여기서 [TeX:] $$F_{\gamma_b}(z)=1-e^{-\frac{z}{\rho_b \theta}} \sum_{k=0}^{m M_b-1}\frac{1}{k!}\left(\frac{z}{\rho_b^\theta}\right)^k$$이다.

따라서 SOP는

로 표현되고, 악의적 UAV의 SNR [TeX:] $$\gamma_e^*$$의 확률밀도함수 (Probability Density Function, PDF)는 다음과 같다:

분석의 용이성을 위해 q(x)를 다음과 같이 정의 하며, q(x)을 이용하면 수식 (1)은 다음과 같다.

최종적으로 아래의 정리를 유도할 수 있다^[5].

3.2 다이버시티 차수 분석

본 절에서는 MRC-Max 스케줄링 기법의 점근적 성 능(asymptotic performance)을 분석하기 위해 보안 다 이버시티 차수(Secrecy Diversity Order, [TeX:] $$d_s$$)를 유도한다. 보안 다이버시티 차수는 높은 주 채널 SNR [TeX:] $$\left(\rho_b\right)$$ 영역에서 보안 아웃티지 확률이 감소하는 속도를 나타내는 척도로, 무선 통신 시스템의 성능을 평가하는 중요한 지표 중 하나이다^[6]. 이는 다음과 같이 정의된다:

다이버시티 차수를 구하기 위해, [TeX:] $$\rho_b \longrightarrow \infty$$ 일 때 [TeX:] $$F_{\gamma_b^*}(z)$$의 점근적 특성을 분석해야 한다. 먼저 [TeX:] $$F_{\gamma_b}(z)$$에서, [TeX:] $$a_b=m M_b$$라 하고, [TeX:] $$u=z\left(\rho_b \theta\right)^{-1}$$로 치환하면, [TeX:] $$F_{\gamma_b}(z)$$은 다음과 같이 표현할 수 있다.

[TeX:] $$\rho_b \rightarrow \infty$$이면 [TeX:] $$\rho_b \rightarrow \infty$$이며, [TeX:] $$u \ll 1$$일 때, [TeX:] $$e^{-u} \text { 와 } \sum_{k=0}^{a_b-1} \frac{u^k}{k!}$$를 테일러 급수(Tayler series)로 전개하여 [TeX:] $$Q(u)$$를 근사하면, 다음과 같이 주어진다^[5].

따라서, 단일 위성 채널 SNR의 CDF는 [TeX:] $$\rho_b \longrightarrow \infty$$일 때 다음과 같이 근사된다.

식 (1)에서, 높은 [TeX:] $$\rho_b$$ 영역에서 [TeX:] $$F_{\gamma_b^*}(z)$$는 다음과 같이 근사할 수 있다.

식 (2)에 위 근사식을 대입하면,

위 식에서 적분 부분은 [TeX:] $$\rho_b$$와 무관한 상수값을 가진다. 따라서,

결론적으로, 제안된 MRC-Max 스케줄링 기법의 보안 다이버시티 차수는 다음과 같다.

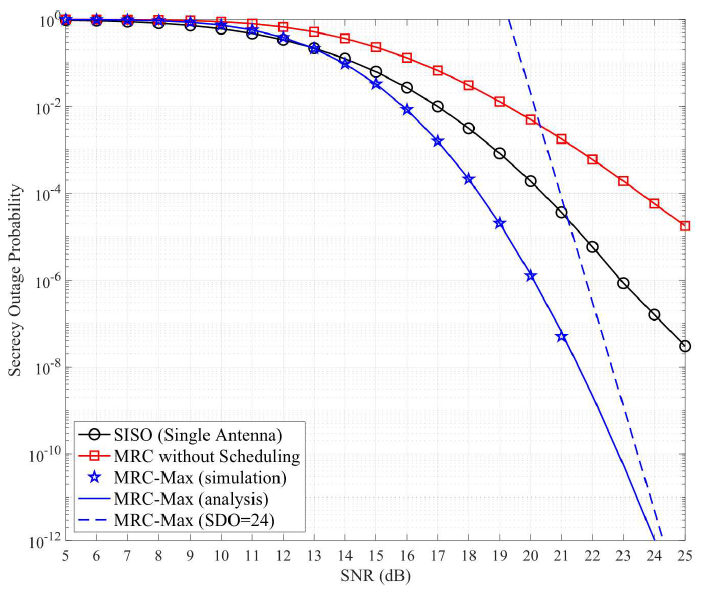
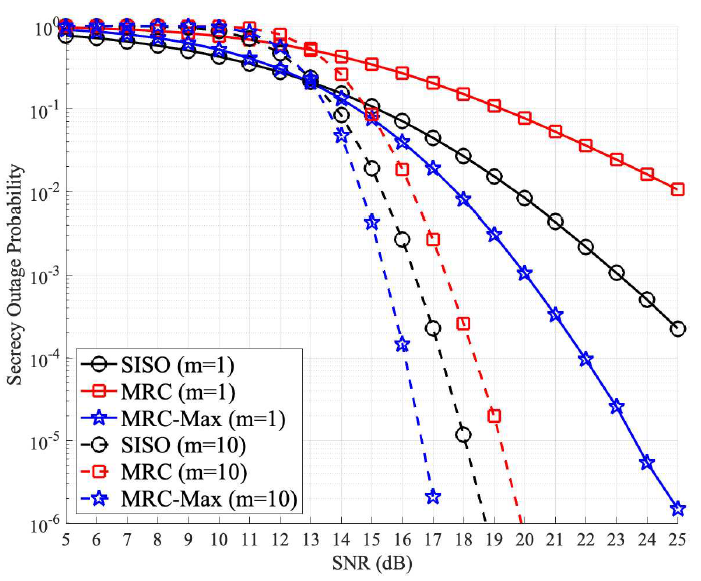
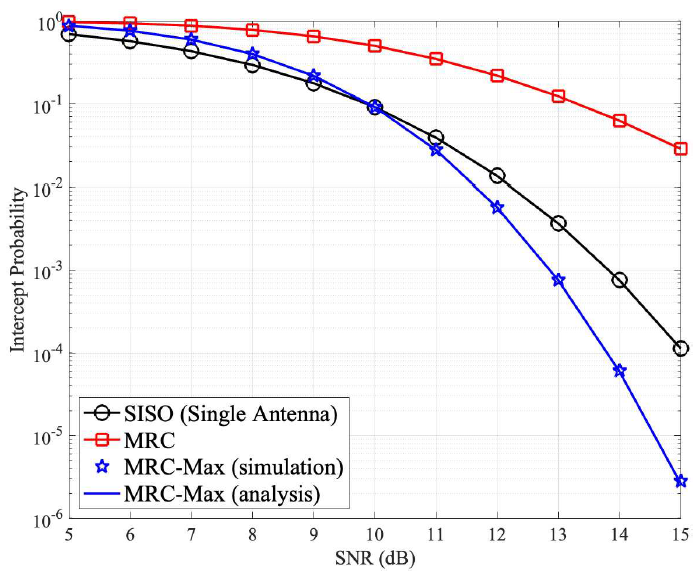
이는 보안 다이버시티 차수가 선택 가능한 위성의 수(N), Nakagami-m 페이딩 파라미터(m), 그리고 GBS의 안테나 수([TeX:] $$M_b$$)의 곱에 비례함을 의미한다.

Ⅳ. 모의실험 결과

본 장에서는 MRC-Max 기법을 두가지 기준 기법과 비교하여 보안 아웃티지 확률(SOP)을 비교한다.

(1) MRC-Max(제안기법): GBS는 MRC 수신기를 사용하고 N개의 후보 위성 중 가장 좋은 위성을 선택한다. 정리 1의 이론적인 성능도 함께 검증한다.

(2) SISO(단일 안테나): 단일 안테나 상황에서 N개의 후보 위성 중 가장 좋은 위성을 선택한다.

(3) MRC: 스케줄링 없이 MRC 수신기를 사용한다. 그림 1의 모의실험에서는 Nakagami-m 매개변수를 m=3, Ω=1, [TeX:] $$M_b=2$$로 설정하고, UAV의 SNR은 [TeX:] $$\rho_e=10 d B$$로 고정한다. 또한, 보안 전송률 요구사항은 [TeX:] $$R_0=1 b p s / H z,$$ 군집 위성의 수는 N=4, 반복 횟수는 [TeX:] $$10^8$$으로 설정한다. GBS의 SNR [TeX:] $$\rho_b$$의 변화에 따른 SOP 성능을 살펴봤을 때 MRC-Max 기법이 단일 안테나 및 MRC 기법에 비해 더 우수한 보안 성능을 달성하는 것을 확인할 수 있다. 또한 정리 1의 유도 결과가 모의실험 결과와 일치하는 것과 SNR [TeX:] $$\rho_b$$ 값이 커질 때 다이버시치 차수 [TeX:] $$d_s=N m M_b=24$$의 근사 성능을 달성할 수 있다는 것을 함께 확인할 수 있다.

그림(Fig.) 1.

SNR에 따른 보안 아웃티지 확률(SOP) (SOP with SNR)

그림 2의 모의실험에서는 Nakagami-m 매개변수를 m=1과 m=10인 두 경우를 고려하고 있으며, 이외의 설정값은 그림 1과 동일한 값을 사용한다. 모의실험 결과 LoS 성분이 강할수록(즉, m값이 큰 경우) 모든 기법의 SOP 성능이 우수한 것을 확인할 수 있다. 또한 다양한 m값을 통해 위성 통신 상황에서 발생할 수 있는 무선 채널의 통계적 불확실성을 반영한 모의실험이 가능하다는 것을 확인할 수 있다. 따라서 실제 위성 통신 운영에 상황을 모델링하는 m값의 범위(예: 1~10)를 추정할 경우 이를 토대로 목표 SOP 성능을 달성하기 위한 보안 전송 기법의 활용 방안을 추가적으로 논의해 볼 수 있다.

그림(Fig.) 2.

m값에 따른 보안 아웃티지 확률(SOP) (SOP with different m values)

그림 3의 모의실험은 보안 전송률 요구사항을 제외한 나머지 설정 값이 그림 1의 설정 값과 동일한 설정 값을 사용하고, 보안 전송률 요구사항이 0인 가로채기 확률의 결과를 나태난다. 군집 위성의 수는 N=10, UAV의 SNR을 [TeX:] $$\rho_e=10 \mathrm{~dB} .$$으로 설정하고 지상국의 채널 링크의 SNR은 UAV의 SNR과 비슷한 수준(5~15 dB)으로 설정했을 때 위성 스케줄링을 사용할 경우 (MRC-Max, SISO), 스케줄링을 사용하지 않은 경우와 비교했을 때 악의적 사용자의 가로채기 확률을 현저히 줄일 수 있는 것을 확인할 수 있다.

그림(Fig.) 3.

SNR에 따른 가로채기 확률 (Intercept probability with SNR)

Ⅴ. 결 론

본 논문은 LEO 위성 네트워크에서 스케줄링 방식에 따른 SOP를 분석하고, Nakagami-m 페이딩 채널에서 SOP의 폐쇄형 표현과 이론적 SDO를 유도하였다. 본 논문에서 도출한 정리 1의 결과를 통해 위성 통신 상황에서 다중 안테나와 위성 스케줄링이 보안 성능에 미치는 영향을 수식적으로 분석하고, 다이버시티 차수 분석 결과를 통해 시스템 설정 값에 따라 직관적으로 이해 가능한 근사적 성능(SDO)을 도출하였다.