IndexFiguresTables |
Sungyeol Back♦ , Chansoo Park* , Youngjun Ko* and Wangrok Oh°Two Stage Early Stopping Belief Propagation Decoding Scheme for Polar CodesAbstract: Early stopping belief propagation (ESBP) decoding scheme was proposed to mitigate the high computational complexity and large decoding latency of belief propagation (BP) decoding scheme. G-matrix based ESBP, compared to previously proposed ESBP, achieves the lowest average number of iterations and excellent frame error rate performance. On the other hand, G-matrix based ESBP requires relatively high complexity for early stopping test. In this paper, we propose an ESBP that adds an additional step to determine whether to perform the G-matrix based ESBP test or not. The proposed scheme achieves the same frame error rate performance compared to G-matrix based ESBP with lower decoding and stopping criterion test complexities. Keywords: Polar Codes , Belief Propagation Decoding Scheme , Early Stopping 백성열♦, 박찬수*, 고영준*, 오왕록°이 단계 극 부호 조기 종료 신뢰 전파 복호 기법요 약: 극 부호 (polar code)의 반복 복호 기법인 조기 종료 신뢰 전파 (early stopping belief propagation, ESBP) 복호 기법은 신뢰 전파 (belief propagation, BP) 복호 기법의 높은 연산 복잡도와 긴 복호 지연 시간을 완화하기 위해 제안되었다. ESBP 복호 기법 중 하나인 G-matrix 기반 ESBP는 가장 적은 평균 반복 복호 횟수와 우수한 프레임 오율 (frame error rate) 성능을 보이나 조기 종료 판별에 요구되는 복잡도가 높은 단점이 있다. 본 논문에서는 G-matrix 조기 종료 판별 수행 여부를 판단하는 단계를 추가한 ESBP를 제안한다. 제안하는 기법은 G-matrix 기반 ESBP와 동일한 프레임 오율 성능을 달성하는 동시에 복호 및 조기 종료 판별에 요구되는 연산 복잡도를 크게 낮출 수 있다. Ⅰ. 서 론극 부호는 BI-DMC (binary input discrete memory- less channel)에서 채널 용량(channel capacity)를 달성 할 수 있다고 이론적으로 증명된 최초의 오류 정정 부호 이다[1]. 극 부호의 복호 방식인 신뢰 전파 (belief prop- agation, BP) 복호 기법[2]은 병렬 복호가 가능하여 연속 제거 (successive cancellation, SC) 복호 기법 대비 복 호 지연 시간이 짧으나 반복 복호 수행으로 인하여 복호 복잡도가 높은 단점이 있다. 이러한 단점을 보완하기 위하여 매 반복 복호 수행 후 특정 조건을 만족하면 복호를 종료하는 다양한 조기 종료 신뢰 전파(early stopping belief propagation, ESBP) 복호 기법들이 제 안되었다[3-8]. 반복 복호를 조기 종료하기 위한 조건으로 G-matrix 와 minLLR(minimum log-likelihood ratio) 기법이 제 안되었다[3]. G-matrix는 매 반복 복호마다 메시지 비트 를 경판정 (hard decision)하여 재부호화(reencoding) 한 결과와 부호 비트에 대한 경판정 결과가 동일한 경우 반복 복호를 종료한다. 반면, minLLR은 메시지 비트 노드(node)에 대한 LLR(log-likelihoodratio)의 절댓 값이 사전에 설정된 임계값 (threshold)을 초과하면 반 복 복호를 종료한다. 조기 종료 판별에 요구되는 복잡도 를 낮추기 위하여 신뢰도를 기반으로 선별된 일부 고정 비트와 정보 비트를 활용하여 반복 복호 종료 여부를 결정하는 ESBP 복호 기법들이 제안되었다[4-7]. [4]에서 는 상대적으로 낮은 신뢰도 순으로 선별된 정보 비트들 의 경판정된 결과가 특정 반복 복호 횟수동안 유지되면 반복 복호를 종료하는 기법을 제안했다. [5]에서는 매 반복 복호마다 높은 신뢰도 순으로 선별된 고정 비트 노드에 대해 에러 여부를 확인하여 특정 반복 복호 횟수 동안 에러가 발생하지 않을 경우 복호를 종료하는 기법 을 제안했다. [5]와 유사하게 높은 신뢰도를 갖는 일부 고정 비트 노드들에 대한 LLR의 절댓값이 임계값을 초과하고 최소 반복 복호 횟수가 충족된 경우 반복 복호 를 종료하는 기법이 [6]에서 제안되었다. [7]에서는 고 정 및 정보 비트로 구성된 PE(processing element) 중 신뢰도가 낮은 정보 비트가 포함된 일부를 선별하고 선 별된 PE의 오른쪽 두 노드의 LLR의 부호(sign)가 동일 한 상태로 설정된 반복 복호 횟수 동안 유지된 경우 복호를 종료하는 기법이 제안되었다. 이외에도, 팩터 그 래프(factor graph)에서 부호율(code rate)이 1인 하위 극 부호(sub-polar code) 내에 위치한 첫 번째 정보 비트 노드에 대한 메시지의 특징을 활용하여 minLLR 기반 낮은 복잡도의 ESBP가 제안되었다[8]. 이처럼 다 양한 조기 종료 기법들이 제안되고 있는 것을 통해 BP 복호 기법에 요구되는 반복 복호 횟수를 줄여 복호 복 잡도를 낮추는 것이 중요할 뿐만 아니라 조기 종료 판 별에 요구되는 복잡도를 낮추는 것이 필요함을 확인할 수 있다. G-matrix 기반 ESBP는 [4-8]에서 제안된 ESBP 복 호 기법 중 요구되는 평균 반복 복호 횟수가 가장 낮을 뿐만 아니라 가장 우수한 프레임 오율 (frame error rate, FER) 성능을 제공하여 조기 종료 기법의 성능 기준으 로 여겨진다. 이를 통해 G-matrix 기반 ESBP는 최적의 반복 복호 종료 시점을 잘 추정하는 것을 확인할 수 있으나 조기 종료 판별을 위해 재부호화 및 비교 연산 등이 필요하여 조기 종료 판별에 요구되는 연산 복잡도 가 높은 단점이 있다. 해당 복잡도를 줄이기 위해 G-matrix 기반 낮은 구현 복잡도의 ESBP 판별기[9]가 제안되었다. 제안된 판별기는 팩터 그래프에서 부호율 이 0 또는 1인 하위 극 부호에 속한 노드들의 LLR 특성 을 이용하여 조기 종료를 판별한다. 해당 판별기는 G-matrix 기반 ESBP와 비교하여 보다 낮은 조기 종료 판별 복잡도를 달성하고 동일한 FER 성능을 보이지만 여전히 매 반복 복호마다 재부호화로 인한 지연 시간이 길며 조기 종료 판별에 필요한 연산 복잡도가 높다. G-matrix 기반 조기 종료 기법은 엄격한 조기 종료 기준으로 최적의 반복 복호 종료 시점을 추정하는 것으 로 알려져 있으나 초기 반복 복호 과정에서는 메시지 비트와 부호 비트 노드의 신뢰도가 낮아 해당 조기 종료 기준을 만족하지 못하며 이러한 초기 반복 복호 과정에 서도 높은 복잡도의 조기 종료 판별이 수행되는 문제가 있다. 따라서 반복 복호 과정에서 G-matrix 기반 조기 종료 판별 수행이 필요한 정도로 팩터 그래프 내의 메시 지들의 신뢰도가 높아졌다고 판단될 경우에만 G-ma- trix 기반 조기 종료 판별을 수행함으로써 조기 종료 판별 성능을 유지하면서 요구되는 복잡도를 낮출 수 있다. 본 논문에서는 G-matrix 조기 종료 판별 수행 여부를 판단하는 단계를 추가하여 조기 종료 판별에 필요한 복 잡도를 낮추는 기법을 제안한다. 제안하는 기법은 매 반복 복호마다 팩터 그래프 내 일부 노드에서 특정 조건 을 만족한 경우에만 G-matrix 기반 조기 종료 판별을 수행한다. 제안하는 기법은 G-matrix 기반 ESBP의 FER 성능을 유지하는 동시에 유사한 평균 반복 복호 횟수 성능을 제공하며 조기 종료 판별 횟수를 줄여 조기 종료 판별에 요구되는 복잡도와 지연 시간을 낮출 수 있다. 또한, 반복 복호 과정에서 팩터 그래프의 모든 메시지를 업데이트하는 대신 G-matrix 기반 조기 종료 판별 수행 여부를 결정짓는 메시지들만 업데이트하여 G-matrix 기반 조기 종료 판별 수행 여부를 결정할 수 있어 복호 복잡도를 추가로 낮출 수 있다. 본 논문의 구성은 다음과 같다. 먼저 2장에서는 본 논문에서 고려하는 시스템 모델과 극 부호의 ESBP 복 호 기법을 설명한다. 3장에서는 제안하는 기법을 설명 하고 4장에서는 제안하는 기법의 성능을 확인하며 5장 에서 결론을 맺는다. Ⅱ. 시스템모델2.1 극부호극 부호의 설계 과정에서는 채널 양극화(channel polarization)를 통해 K개의 정보 비트와 (N-K)개의 고정 비트를 메시지 비트에 매핑하기 위한 인덱스 집합 I와 Ic를 도출한다[1,10]. 메시지 벡터 (message vector) [TeX:] $$\begin{equation} \mathbf{u}=\left\{u_0, u_1, \cdots, u_{N-1}\right\} \end{equation}$$ 내의 uk,k∈I에는 정보 비트가 매핑되며 uk,k∈Ic에는 고정 비트로서 ‘0’이 매핑된다. 길이가 N인 극 부호어 [TeX:] $$\begin{equation} \mathbf{c}=\left\{c_0, c_1, \cdots, c_{N-1}\right\} \end{equation}$$는 식 (1) 과 같이 생성 행렬 GN을 통해 생성되며 여기에서 GN 은 [TeX:] $$\begin{equation} \mathrm{F}=\left[\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right] \end{equation}$$의 n = log2N차 크로네커 제곱 (Kronecker power) 연산을 통해 구할 수 있다.
생성된 극 부호어 c는 식 (2)와 같이 BPSK (binary phase shift keying) 심볼 sk로 변조된 후 양대역 전력 밀도가 [TeX:] $$\begin{equation} \frac{N_0}{2} \end{equation}$$인 가산성 백색 잡음 (addictive white Gaussian noise, AWGN) 채널을 통해 수신기로 전송된 다.
수신기에서는 수신 신호 yk=sk+ηk를 통해 부호 비트 ck에 대한 LLR을 식 (3)과 같이 계산한 후 극 부호 복호기의 입력값으로 사용한다. 이때 ηk는 평균과 분산 이 각각 0과 [TeX:] $$\begin{equation} \frac{N_0}{2} \end{equation}$$인 가우시안 랜덤 변수를 나타낸다.
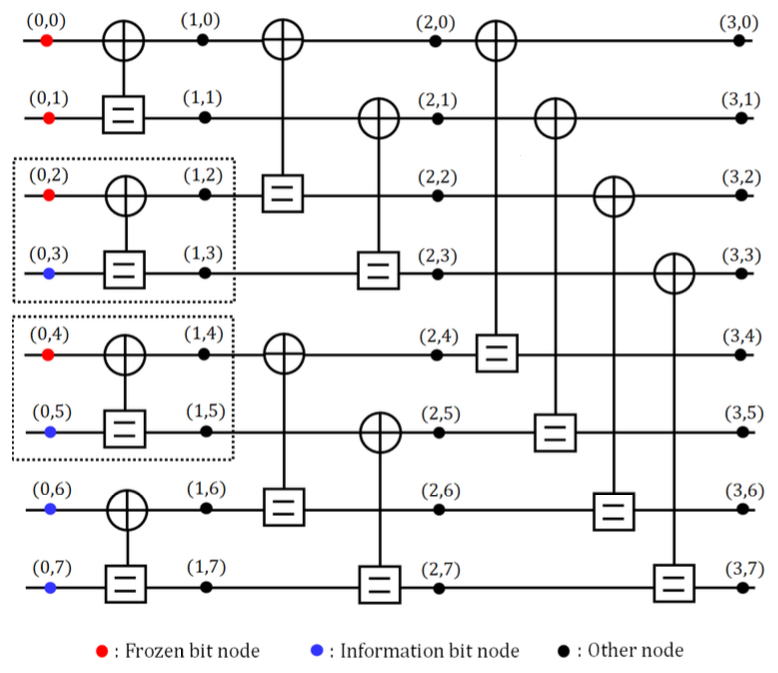
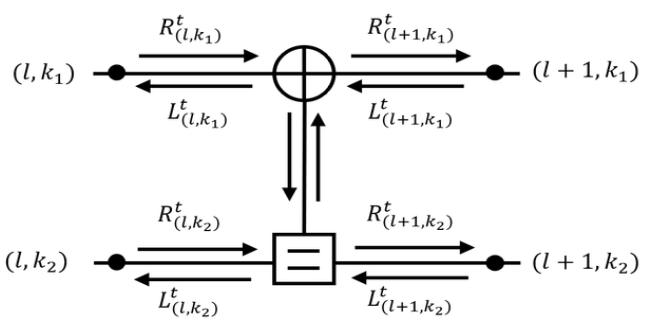
(3)[TeX:] $$\begin{equation} L\left(c_k \mid y_k\right)=\ln \frac{P\left(c_k=0 \mid y_k\right)}{P\left(c_k=1 \mid y_k\right)}, k=0,1, \cdots, N-1 \end{equation}$$2.2 BP 복호 기법길이 N=8인 경우 극 부호의 BP 복호를 위한 팩터 그래프를 도식화하면 그림 1과 같다. 그림 1에서 [TeX:] $$\begin{equation} (l,k),l \in\left\{0,1, \cdots, \log _2 N\right\}, k \in\{0,1, \cdots, N-1\} \end{equation}$$는 l 단계에 서 k 번째 노드를 나타내며 [TeX:] $$\begin{equation} (0, j), j \in I^c \end{equation}$$ 노드는 고정 비트 노드를 [TeX:] $$\begin{equation} (0, j), j \in I \end{equation}$$ 노드는 정보 비트 노드를 나타 낸다. 그림 1에서 볼 수 있는 바와 같이 팩터 그래프의 각 단계는 그림 2에 나타낸 PE가 [TeX:] $$\begin{equation} \frac{N}{2} \end{equation}$$개로 구성된다. 그림 2에서 [TeX:] $$\begin{equation} R_{(l, k)}^t, \quad L_{(l, k)}^t \end{equation}$$는 t번째 반복 복호 과정에서 각각 우측 방향, 좌측 방향으로 계산된 (l,k) 노드의 LLR을 나타내며 식 (4)와 같이 계산할 수 있다.
(4)[TeX:] $$\begin{equation} \begin{aligned} & R_{\left(l+1, k_1\right)}^t=f\left(R_{\left(l, k_1\right)}^t, R_{\left(l, k_2\right)}^t+L_{\left(l+1, k_2\right)}^{t-1}\right) \\ & R_{\left(l+1, k_2\right)}^t=f\left(R_{\left(l, k_1\right)}^t, L_{\left(l+1, k_1\right)}^{t-1}\right)+R_{\left(l, k_2\right)}^t \\ & L_{\left(l, k_1\right)}^t=f\left(L_{\left(l+1, k_1\right)}^t, R_{\left(l, k_2\right)}^t+L_{\left(l+1, k_2\right)}^t\right) \\ & L_{\left(l, k_2\right)}^t=f\left(R_{\left(l, k_1\right)}^t, L_{\left(l+1, k_1\right)}^t\right)+L_{\left(l+1, k_2\right)}^t \end{aligned} \end{equation}$$이때 f(·)는 식 (5)와 같으며 sgn(·)은 부호 함수 (sign function)를 나타내고 식 (6)와 같이 설정된 [TeX:] $$\begin{equation} R_{(l, k)}^0, L_{(l, k)}^0 \end{equation}$$가 초기값으로 사용된다.
(5)[TeX:] $$\begin{equation} \begin{aligned} f(a, b) & =2 \tanh ^{-1}(\tanh (a / 2) \tanh (b / 2)) \\ & \approx \operatorname{sgn}(a) \operatorname{sgn}(b) \min (|a|,|b|) \end{aligned} \end{equation}$$
(6)[TeX:] $$\begin{equation} \begin{aligned} R_{(l, k)}^0 & = \begin{cases}\infty, & l=0, k \in I \\ 0, & \text { otherwise }\end{cases} \\ L_{(l, k)}^0 & = \begin{cases}L\left(c_k \mid y_k\right) & , l=\log _2 N, k=0,1, \ldots, N-1 \\ 0 & , \text { otherwise }\end{cases} \end{aligned} \end{equation}$$매 반복 복호에서 [TeX:] $$\begin{equation} R_{(l, k)}^t \end{equation}$$을 1단계에서 log2N단계까지 최신화한 다음 [TeX:] $$\begin{equation} L_{(l, k)}^t \end{equation}$$을 log2N-1단계부터 0단계까지 최신화하며 이와 같은 반복 복호를 최대 반복 복호 횟수 인 Im만큼 수행하고 식 (7)과 같이 정보 비트 [TeX:] $$\begin{equation} \hat{u}_k^{I_{\mathrm{m}}}, k \in I \end{equation}$$ 를 추정한다.
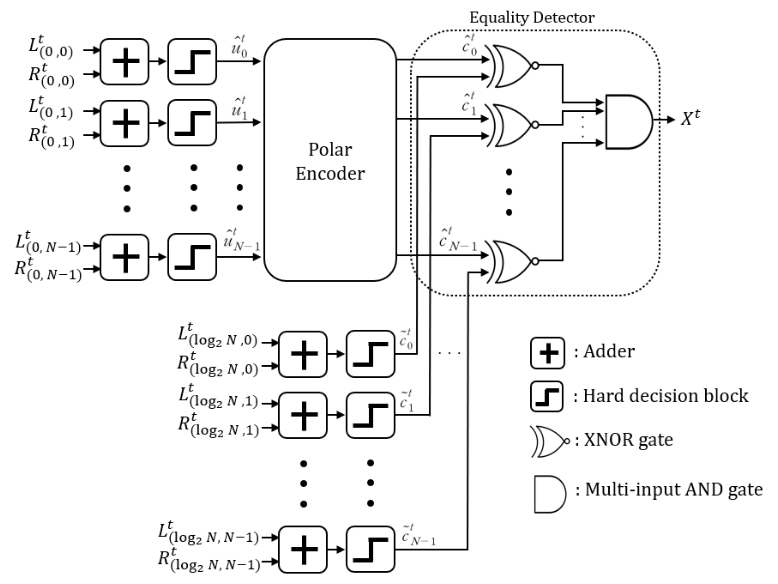
(7)[TeX:] $$\\begin{equation} \hat{u}_k^{I_{\mathrm{m}}}=\left\{\begin{array}{l} 0, L_{(0, k)}^{I_{\mathrm{m}}}+R_{(0, k)}^{I_{\mathrm{m}}} \geq 0 \\ 1, \text { otherwise } \end{array} .\right. \end{equation}$$2.3 G-matrix 기반 ESBP 복호 기법BP 복호 기법은 Im번 만큼 반복 복호를 수행하여야 하며 이에 따라 연산 복잡도가 높은 문제가 있다. 해당 문제를 해결하기 위해 G-matrix 기반 ESBP가 제안되 었다[3]. G-matrix 기반 ESBP는 매 반복 복호가 종료될 때마다 [TeX:] $$\begin{equation} L_{(0, k)}^t+R_{(0, k)}^t, k=0,1, \ldots, N-1 \end{equation}$$를 경판정한 메 시지 벡터 [TeX:] $$\begin{equation} \hat{\mathbf{u}}^t=\left[\hat{u}_0^t, \hat{u}_1^t, \cdots, \hat{u}_{N-1}^t\right] \end{equation}$$를 GN을 통해 재부호 화하여 [TeX:] $$\begin{equation} \hat{\mathbf{c}}^t=\left[\hat{c}_0^t, \hat{c}_1^t, \cdots, \hat{c}_{N-1}^t\right] \end{equation}$$를 생성하고 [TeX:] $$\begin{equation} L_{\left(\log _2 N, k\right)}^t+R_{\left(\log _2 N, k\right)}^t, k=0,1, \cdots, N-1 \end{equation}$$를 경판정한 [TeX:] $$\begin{equation} \tilde{c}^t=\left[\tilde{c}_0^t, \tilde{c}_1^t, \cdots, \tilde{c}_{N-1}^t\right] \end{equation}$$와 비교하여 [TeX:] $$\begin{equation} \hat{\mathbf{c}}^t=\tilde{\mathbf{c}}^t \end{equation}$$ 조건을 만족 하면 반복 복호를 종료한다. G-matrix 기반 ESBP를 수 행하기 위한 하드웨어 구조와 반복 복호 당 요구되는 연산 복잡도는 각각 그림 3 및 표 1과 같다. 그림 3에 나타낸 경판정기 (hard decision block)는 입력값이 ‘0’ 이상인 경우 ‘0’을 출력하고 미만일 경우 ‘1’을 출력한 다. 동등 판결기(equality detector)는 입력값 [TeX:] $$\begin{equation} \hat{\mathbf{c}}^t, \tilde{\mathbf{c}}^t \end{equation}$$를 원소별로 비교하여 모두 동일한 경우 Xt=1을 출력하 고 그렇지 않을 경우 ‘0’을 출력한다. 매 반복 복호 종료 후 Xt=1인 경우 반복 복호를 종료한다. 표 1. G-matrix 조기 종료 판별기의 연산 복잡도
표 1에서 볼 수 있는 바와 같이 G-matrix를 이용한 조기 종료 판별에 요구되는 연산 복잡도가 높은 문제가 있다[3]. 이를 개선하기 위해 부호율이 0 또는 1인 하위 극 부호에 해당하는 팩터 그래프들을 특정한 다음 각각 의 하위 극 부호 팩터 그래프 내에서 갱신되는 메시지의 특성을 활용하여 구현 복잡도를 줄이는 기법이 제안되 었다[9]. 해당 기법에서는 부호율이 0인 하위 극 부호의 팩터 그래프에서 모든 노드의 LLR 값이 ∞이며 부호 율이 1인 하위 극 부호의 팩터 그래프 내 노드들은 우측 방향으로 계산되는 메시지가 항상 ‘0’에 머물러 있는 특징을 이용한다. 이를 통해 재부호화 과정에서 필요한 덧셈기 및 XOR 연산기 개수를 줄여 구현 복잡도를 낮 출 수 있으나 매 반복 복호마다 재부호화된 극 부호어와 경판정된 부호 비트들의 비교 등에 요구되는 연산 복잡 도가 여전히 높을 뿐만 아니라 조기 종료 판별 과정에서 필요한 재부호화로 인한 지연 시간이 발생하는 문제가 있다. Ⅲ. 제안하는 기법BP 복호 기법에 요구되는 반복 복호 횟수를 낮추기 위해 다양한 조기 종료 기법들이 제안되어 있으나 FER 및 평균 반복 복호 횟수 성능의 경우에는 G-matrix 기 반 ESBP 복호 기법이 가장 우수하다[8]. 그러나 매 반복 복호 종료 후 표 1에 나타낸 바와 같이 조기 종료 판별 에 비교적 높은 연산 복잡도가 요구되는 문제가 있다. 본 논문에서는 불필요한 G-matrix 기반 조기 종료 판별 을 수행하지 않도록 조기 종료 판별 수행 여부 판단 단계를 추가하여 조기 종료 판별에 필요한 연산 복잡도 와 지연 시간을 낮추는 기법을 제안한다. 길이 N인 극 부호의 팩터 그래프는 [TeX:] $$\begin{equation} \frac{N}{2} \log _2 N \end{equation}$$개의 PE로 구성되어 있으며 이 중 일부 PE는 좌측 상단 및 하단 노드에 고정 비트와 정보 비트가 각각 매핑되어 있다. 이처럼 고정 및 정보 비트로 구성된 PE를 FIPE (frozen and information processing element)[7]라 하며 FIPE의 고정 비트들의 노드 인덱스를 원소로 갖는 집합 S를 생성할 수 있다. 예로 들어 그림 1에서 N=8 , K=4 및 I={3,5,6,7}인 경우 점선으로 표시된 PE 는 FIPE를 나타내며 이때 S={2,4}이다. FIPE가 고 정 비트와 정보 비트로 구성된 특성으로 인하여 반복 복호 과정에서 FIPE의 정보 비트 노드들이 성공적으로 복호되기 위해서는 [TeX:] $$\begin{equation} L_{(1, k)}^t \end{equation}$$와 [TeX:] $$\begin{equation} L_{(1, k+1)}^t, k \in \mathbf{S} \end{equation}$$가 동일한 부호를 가져야 한다. 해당 특징을 이용하여 매 반복 복 호 종료 후 식 (8)에 대한 조건의 만족 여부를 확인한다.
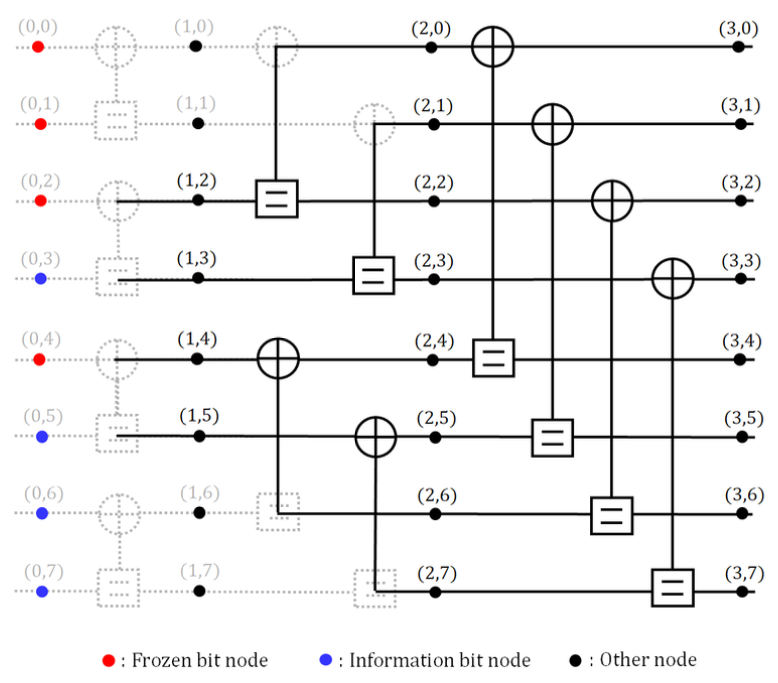
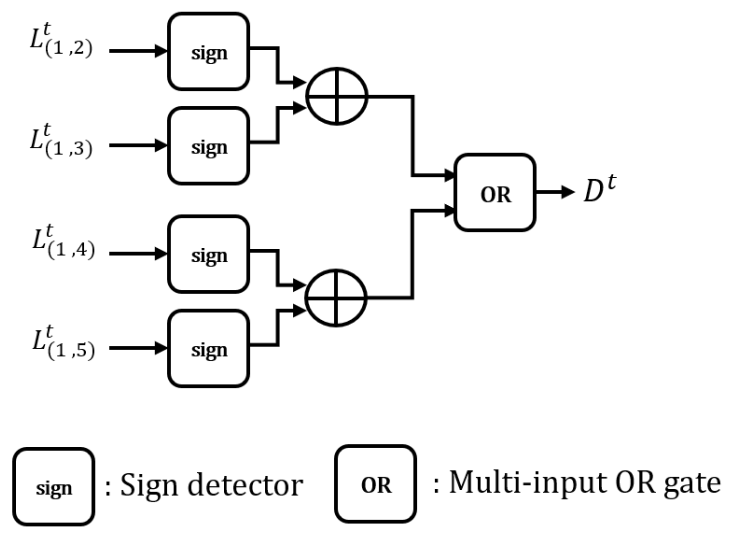
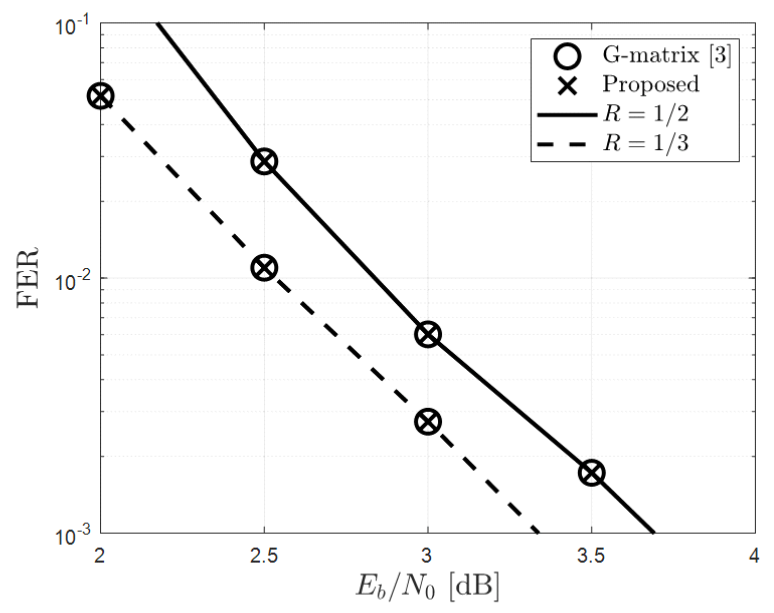
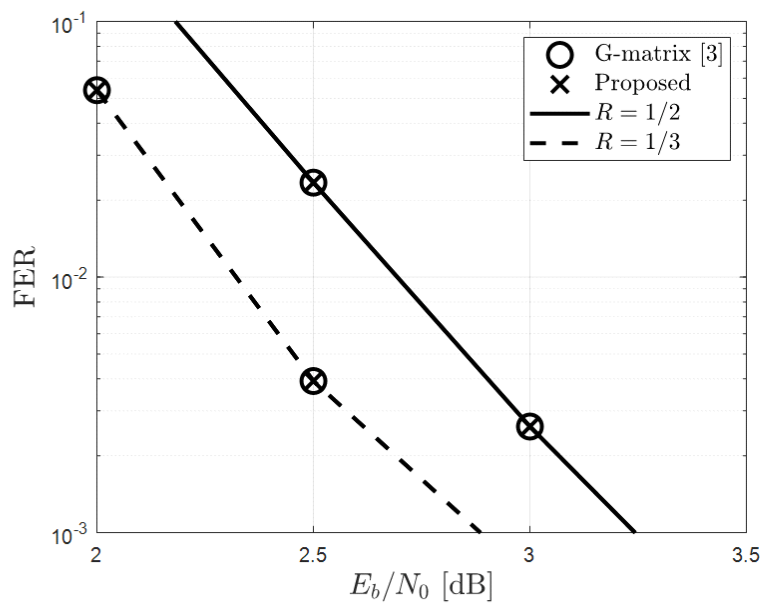
(8)[TeX:] $$\begin{equation} \operatorname{sgn}\left(L_{(1, k)}^t\right)=\operatorname{sgn}\left(L_{(1, k+1)}^t\right), \forall k \in \mathbf{S} . \end{equation}$$해당 조건을 만족하는 경우 G-matrix 기반 조기 종료 판별을 수행하고 그렇지 않을 경우 G-matrix 기반 조기 종료 판별 수행 없이 다음 반복 복호를 수행한다. 이를 통해 반복 복호 과정에서 팩터 그래프 내의 메시지들의 신뢰도가 높아진 경우에서만 G-matrix 기반 조기 종료 판별기를 동작시킴으로써 조기 종료 판별에 요구되는 연산 복잡도와 재부호화에 따른 지연 시간을 낮출 수 있다. 매 반복 복호마다 식 (8)에 대한 조건을 이용하여 G-matrix 조기 종료 판별 수행 여부를 판단할 경우 재 부호화와 비교 연산 등을 생략할 수 있어 모든 메시지 비트에 대한 LLR 값을 업데이트할 필요가 없다. 또한, 그림 1에서 길이 [TeX:] $$\begin{equation} \frac{N}{2^i}, i \in\left\{0,1, \cdots, \log _2 N\right\} \end{equation}$$을 갖는 부호 율이 0 또는 1인 하위 극 부호의 팩터 그래프를 고려할 경우 모든 노드의 우측 방향 LLR 값은 매 반복 복호마 다 ‘∞’ 또는 ‘0’으로 계산된다. 따라서 G-matrix 기반 조기 종료 판별을 수행하지 않을 경우 부호율이 0 또는 1인 하위 극 부호의 팩터 그래프 내에서는 좌측 및 우측 방향 메시지 업데이트를 수행하지 않아도 되며 식 (8)에 대한 조건의 만족 여부를 확인하기 위한 좌측 및 우측 메시지 업데이트가 필요하다. 따라서 그림 4와 같이 기 존 팩터 그래프에서 부호율이 0 또는 1인 하위 극 부호 의 팩터 그래프를 제외한 상태로 매 반복 복호마다 실선 을 따라 식 (8)에 대한 조건의 만족 여부를 판별하기 위한 노드들의 LLR 값들만 업데이트한다. 식 (8)이 만 족된 경우 G-matrix 기반 조기 종료 판별을 위해 점선 으로 표시된 부분에 해당하는 노드들의 LLR 값을 추가 적으로 업데이트하는 방식으로 동작할 수 있으며 이를 통해 식 (8)이 만족되지 않는 반복 복호, 즉 G-matrix 조기 종료 판별을 수행하지 않는 반복 복호에서는 메시 지 업데이트 횟수를 줄여 복호에 필요한 복잡도를 추가 로 낮출 수 있다. 그림 5는 G-matrix 조기 종료 판별 수행 여부를 결정 하는 하드웨어의 구조를 나타낸다. 여기서 부호 판별기 (sign detector)는 입력값의 부호가 ‘+’인 경우 ‘1’을 ‘-’ 인 경우 ‘0’을 출력한다. 매 반복 복호가 종료된 후 Dt 를 출력하여 Dt=0인 경우에만 G-matrix 기반 조기 종료 판별을 수행하며 해당 판별기에서 반복 복호 당 요구되는 연산 복잡도는 표 2와 같으며 여기에서 |S| 는 집합 S의 카디널리티(cardinality)를 나타낸다. 표 2에서 볼 수 있는 바와 같이 비교적 낮은 연산 복잡도로 G-matrix 조기 종료 판별 수행 여부를 판단할 수 있다. 제안하는 기법은 G-matrix 조기 종료 판별 수행 횟수를 줄임으로써 조기 종료 판별에 요구되는 복잡도와 재부 호화에 따른 지연 시간을 낮출 수 있을 뿐만 아니라 G-matrix 조기 종료 판별을 수행하지 않는 반복 복호 과정에서 메시지 업데이트 횟수를 줄여 복호 복잡도를 낮출 수 있다. Ⅳ. 전산 실험 결과제안하는 기법의 성능을 확인하기 위해 전산실험에 사용된 파라미터는 표 3과 같다. 본 논문에서는 극 부호 설계 기법으로 메시지 벡터 내 원소들의 양극화 가중치 (polarization weight)를 계산하여 고정 및 정보 비트들 이 매핑될 위치를 결정하는 β-expansion[10]을 사용하였 으며 Im은 BP 복호 시 더 이상 프레임 오율 성능 개선 이 없는 최솟값으로 설정하였다. 그림 6과 그림 7은 N=512, 1024인 경우 R=1/2, 1/3에 대해 G-matrix 기반 ESBP와 제안하는 복호 기법의 프레임 오율 성능 을 나타낸 것이다. 이때 Eb는 정보 비트 당 에너지를 나타낸다. 그림 6과 그림 7에서 볼 수 있는 바와 같이 제안하는 복호 기법은 고려한 모든 환경에서 G-matrix 기반 ESBP와 동일한 프레임 오율 성능을 보임을 확인 할 수 있다. 표 3. 전산실험 파라미터
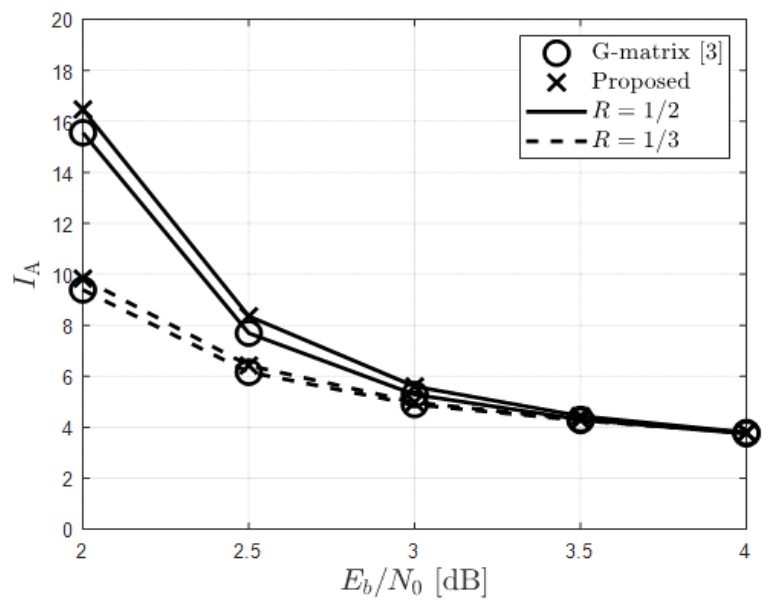
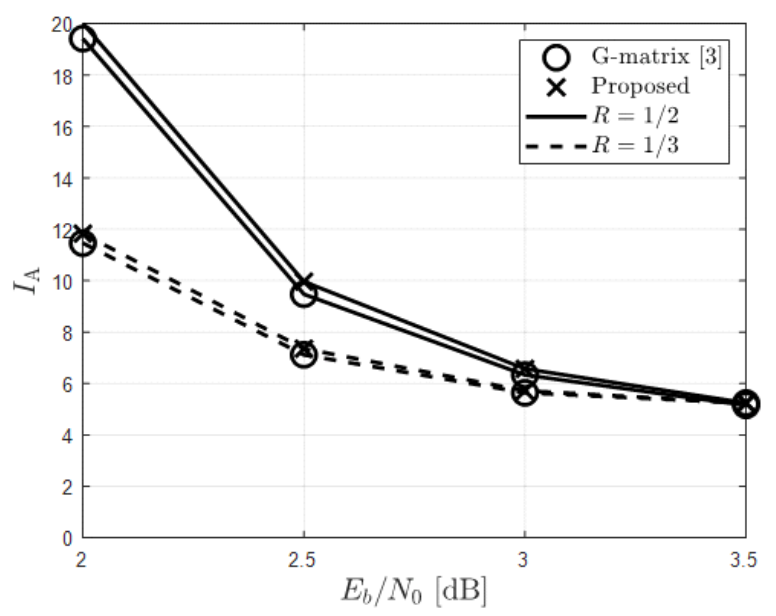
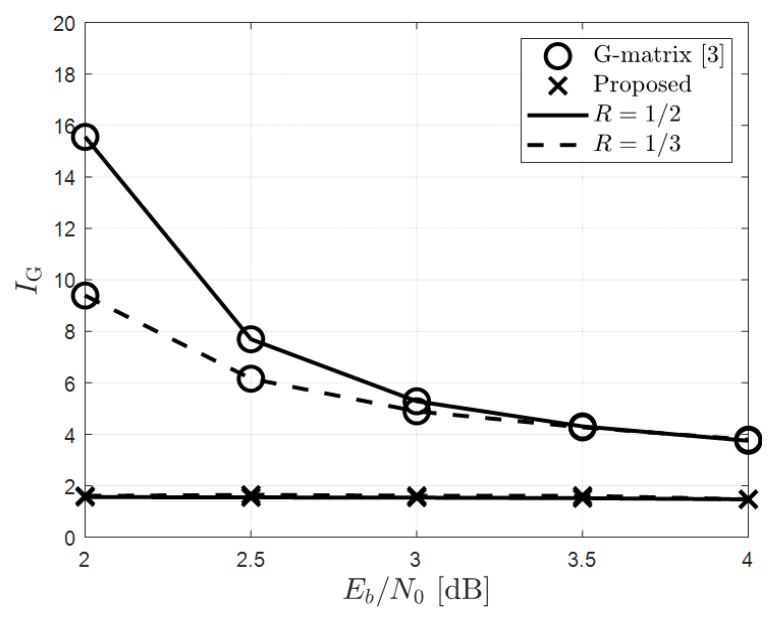
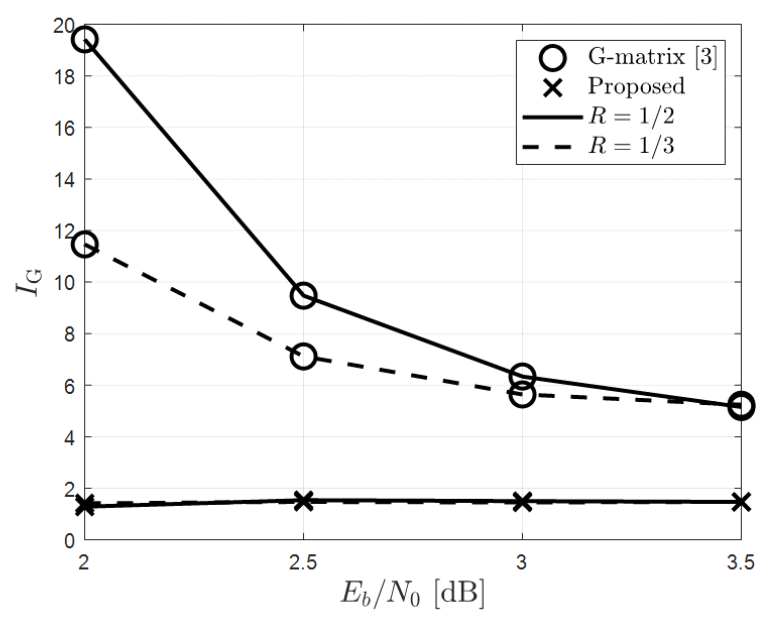
G-matrix 기반 ESBP와 제안하는 복호 기법의 복호 지연 시간을 확인하기 위해 N=512, 1024, R=1/2, 1/3에 대해 평균 반복 복호 횟수 IA와 평균 G-matrix 조기 종료 판별 횟수 IG를 각각 도출하였으며 그 결과는 그림 8-11과 같다. 그림 8-11을 통해 프레임 오율이 10-3을 달성하는 동작 환경에서 G-matrix 기반 ESBP와 제안하는 복호 기법의 IA와 IG를 표 4에 나타 내었다. 표 4에서 볼 수 있는 바와 같이 제안하는 복호 기법의 IA는 고려한 모든 환경에서 G-matrix 기반 ESBP의 IA와 유사하여 복호 지연 시간이 크게 증가하 지 않음을 확인할 수 있다. 제안하는 기법은 고려한 모 든 환경에서 IG가 2 미만 으로 기존 기법 대비 G-matrix 조기 종료 판별 횟수가 감소하였고 이에 따라 조기 종료 판별기에 요구되는 연산 복잡도와 재부호화에 따른 지 연 시간을 크게 줄일 수 있다. 프레임 오율이 10-3을 달성하는 동작 환경에서 G-matrix 기반 ESBP 대비 제안하는 기법의 복호 복잡 도 및 G-matrix 조기 종료 판별기에 요구되는 연산 복 잡도 감소율을 확인하였으며 이를 표 5에 나타내었다. 표 5에서 볼 수 있는 바와 같이 제안하는 기법은 고려한 모든 환경에 대해 복호 복잡도 및 G-matrix 조기 종료 판별에 요구되는 연산 복잡도를 각각 최대 31.1 및 76.3%만큼 줄일 수 있다. 이와 더불어 본 논문에서 제 안하는 기법은 G-matrix 기반 조기 종료 판별 복잡도를 줄이기 위해 제안된 기법[9]에도 그대로 적용되어 G-matrix 조기 종료 판별 횟수를 줄일 수 있으며 해당 기법과 비교하더라도 표 5에 나타낸 동일한 비율로 복 잡도를 추가로 줄일 수 있다. BiographyBiographyBiographyReferences
|
StatisticsCite this articleIEEE StyleS. Back, C. Park, Y. Ko, W. Oh, "Two Stage Early Stopping Belief Propagation Decoding Scheme for Polar Codes," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 6, pp. 924-932, 2025. DOI: 10.7840/kics.2025.50.6.924.
ACM Style Sungyeol Back, Chansoo Park, Youngjun Ko, and Wangrok Oh. 2025. Two Stage Early Stopping Belief Propagation Decoding Scheme for Polar Codes. The Journal of Korean Institute of Communications and Information Sciences, 50, 6, (2025), 924-932. DOI: 10.7840/kics.2025.50.6.924.
KICS Style Sungyeol Back, Chansoo Park, Youngjun Ko, Wangrok Oh, "Two Stage Early Stopping Belief Propagation Decoding Scheme for Polar Codes," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 6, pp. 924-932, 6. 2025. (https://doi.org/10.7840/kics.2025.50.6.924)
|