IndexFiguresTables |
Taehee Choi♦ , Jaehong Kim* and Jingon Joung°Encoding-Rule-Candidate Group Design for Security Rate Enhancement of Space-Time Line Code Hopping SystemsAbstract: In conventional space-time line code (STLC) systems with eavesdroppers (Eve), the security performance is significantly degraded when the user and Eve channels are highly correlated. An STLC hopping scheme was recently proposed to overcome this limitation, where an encoding rule is randomly selected from a candidate group for every two symbols, resulting in decoding failure for Eve. Here, the optimal encoding rule candidate group can be designed by selecting rules that achieve high secrecy rates, and the optimal candidate group is dependent on the channel correlation factor. In this study, we propose two design methods, depending on whether the transmitter knows the channel correlation factor. Simulation results show that the proposed scheme achieves optimal performance if the correlation information is provided. When the correlation factor is unknown to the transmitter, the STLC hopping scheme with the proposed method achieves a secrecy rate of over 95.5% of the maximum secrecy rate achieved by an optimal STLC hopping scheme. Keywords: Space-time line code (STLC) , code hopping , secure communications 최태희♦, 김재홍*, 정진곤°시공간 선 부호 호핑 시스템 보안 전송률 향상을 위한 부호화 규칙 후보군 설계요 약: 기존 시공간 선 부호(STLC: space-time line code) 시스템은 도청자가 존재하고, 도청자 채널과 사용자 채널 사이 상관도가 높을 때 보안 성능이 크게 열화된다. 최근, 이를 해결하기 위해, 두 심볼마다 송신기가 부호화 규칙후보군에서 부호화 규칙을 무작위로 선택하여 도청자가 복호화를 성공적으로 수행할 수 없도록 하는 STLC 호핑기법이 제안되었다. 이때, 보안 전송률이 높은 일부 부호화 규칙만을 선별하여 최적 부호화 규칙 후보군을 만들수 있으며, 최적 부호화 규칙 후보군은 사용자와 도청자 채널 간 상관 계수에 따라 바뀌게 된다. 이에 착안하여, 본 연구에선 송신기가 도청자와 사용자 사이 채널 상관 계수를 알고 있는 경우와 알 수 없는 경우 각각 적용할수 있는 두 가지 부호화 규칙 후보군을 설계한다. 모의실험 결과, 제안한 부호화 규칙 후보군을 사용한 STLC 호핑 기법이 기존 방식 대비 높은 보안 전송률을 얻으며, 특히, 송신기가 채널 상관 계수를 알 경우, 최적 보안 전송률을 달성할 수 있음을 확인하였다. 한편, 송신기가 채널 상관 계수를 알 수 없을 때는 설계한 STLC 호핑 기법이 최적 STLC 호핑 기법의 95.5%에 달하는 보안 전송률을 얻을 수 있음을 확인하였다. Ⅰ. 서 론차세대 무선통신 네트워크의 보안 성능을 향상하는 방법으로 물리 계층 보안 기술이 활발히 연구되고 있다[1,2]. 예를 들어, 빔포밍 설계, 인공 잡음 기반 보안 통신 기술, 주파수 호핑 기술이 연구되었으며[3-5], 시공간 블록 부호화 (STBC: space-time block code)와 시공간 선 부호화 (STLC: space-time line code) 같은 공간 다이버시티 기법에 보안 성능을 향상하는 기술이 적용된 바 있다[6,7]. 하지만, 주파수 호핑 기술은 송신기에서 주파수 합성기를 통한 빠른 주파수 변경과 수신기에서 정확한 동기화가 필요하므로 하드웨어 복잡도가 증가할 수 있으며, 전대역을 사용하는 시스템 대비 낮은 주파수 효율을 갖는다. 또한, 기존 연구에선 사용자와 도청자 채널 간 상관관계가 없는 이상적인 상황을 가정하였지만, 실제 환경에선 사용자와 도청자 채널 사이에 상관관계가 존재할 수 있다[8]. 특히, 빔포밍과 인공 잡음 기반 보안 성능 향상 기술은 사용자와 도청자 채널 사이에 상관관계가 존재하는 경우 보안 통신 성능이 저하된다[9,10]. STLC는 STBC와 대칭인 기법으로, 송신기는 전체 채널 상태 정보 (CSI: channel state information)을 써 STLC 심볼을 변조하며, 수신기는 부분 CSI만을 활용한 선형 결합을 통해 정보 심볼을 복호화한다[11]. STLC는 간단한 수신기 구조로 최대 다이버시티 이득을 얻을 수 있어, 다중 사용자 통신[12], 협력 통신[13], 차량 통신[14], 지능형 반사 표면[15]과 같은 다양한 무선 시스템에 적용되어 활발히 연구되고 있다. STLC 시스템이 갖는 보안 성능을 높이기 위한 기존 연구에선 도청자 채널에 인공 잡음을 추가하는 방식이 제안되었다[7]. 해당 기술은 인공 잡음을 통해 도청자 통신 성능을 열화시킬 수 있으나, 송신기 측에 다중 안테나를 요구하므로 한 개 송신 안테나와 두 개 수신 안테나를 사용하는 1 × 2 STLC 시스템에 적용할 수 없다. 또한, 송신 신호 전력 중 일부를 인공 잡음 신호에 할당하므로 데이터 전송률 성능이 낮아질 수 있다. 기존 STLC 시스템은 사용자와 도청자 채널 사이 상관도가 높은 상황에서 보안 성능이 심각하게 저하되며, 이러한 한계를 극복하기 위해 STLC 호핑 기법이 제안되었다[16]. STLC 호핑 기법에서 송신기는 두 정보 심볼마다 부호화 규칙 후보군에서 무작위로 STLC 부호화 규칙을 선택하여 정보 심볼을 부호화하고 전송한다. 수신기 측 복호화 규칙은 송신기가 선택한 부호화 규칙에 따라 유일하게 결정되며, 사용자는 송신기와 부호화 규칙을 공유하여 올바른 규칙으로 정보 심볼을 복호화한다. 이때, 부호화 규칙 공유는 사용자 인증 과정에서 송신기와 사용자 간 공유되는 키를 의사 난수 생성기의 초깃값으로 사용하여 수행할 수 있다[17, 18]. 반면, 도청자는 무작위 부호화 규칙에 따른 복호화 규칙을 알지 못하므로, 도청자가 얻는 수신 신호 대 잡음비 (SNR: signal-to-noise ratio) 성능이 열화된다. 이를 통해, STLC 호핑 기법은 사용자와 도청자 채널 사이 상관 계수가 높은 상황에서도 우수한 보안 성능을 제공할 수 있다. 추가로, STLC 호핑 기법은 의사난수 생성기와 스위치를 통해 간단하게 기존 시스템에 적용할 수 있다. 송신기가 선택할 수 있는 부호화 규칙 후보가 많을수록 도청자가 올바른 복호화 규칙을 사용할 확률이 낮아진다. 하지만, 전체 부호화 규칙 중 상대적으로 낮은 보안 성능을 갖는 규칙이 존재하므로, 전체 부호화 규칙을 후보로 사용하면 STLC 호핑 시스템의 평균 보안 성능이 저하된다. 따라서, 전체 부호화 규칙 중 보안 성능을 효과적으로 높이는 부호화 규칙을 일부 선정하여 최적 부호화 규칙 후보군을 설계할 수 있다. 본 연구에선 STLC 호핑 시스템의 보안 성능을 최대화하기 위해, 송신기가 사용자와 도청자 채널 사이 상관 계수를알 때 사용할 수 있는 최적 부호화 규칙 후보군 설계 방식과 채널 상관 계수를 알 수 없을 때 사용할 수 있는 준 최적 부호화 규칙 후보군을 설계 방식을 제안한다. 모의실험 결과, 사용자와 도청자 채널 사이 상관도가 높은 상황에서도 STLC 호핑 시스템은 우수한 보안 성능을 제공하였으며, 송신기가 채널 상관 계수를 알 때, 최적 보안 전송률 하한 (SRLB: secrecy rate lower bound) 성능을 달성하였다. 또한, 송신기가 채널 상관 계수를 알 수 없을 때는 설계한 STLC 호핑 기법이 최적 STLC 호핑 기법에 근접한 SRLB 성능을 가짐을 확인하였다. 본 논문에선 STLC 호핑 시스템 연구를 다음과 같은 구성으로 서술한다. 2장에선 보안 통신 관점에서 기존 STLC 시스템을 분석한다. 3장에선 기존 STLC 시스템의 취약점을 극복하기 위한 STLC 호핑 기법을 설명하고 부호화 규칙 후보군 설계 방식을 제안한다. 4장에선 설계한 STLC 호핑 시스템의 성능을 확인하는 모의실험 결과를 제시하고 5장에서 본 논문을 마무리한다. 위 첨자 ‘∗’와 ‘T’는 각각 행렬과 벡터에 대한 복소 켤레와 전치 연산자를 의미하며, E[X]는 확률 변수 X에 대한 기댓값이다. [TeX:] $$C N\left(\mu, \sigma^2\right)$$은 평균이 μ고 분산이 [TeX:] $$\sigma^2$$인 복소 정규 분포를 의미하며, [TeX:] $$\mathfrak{I}(x)$$는 복소수 x의 허수 부분을 의미한다. [TeX:] $$(x)^{+}$$는 max(0,x)를 의미한다. Ⅱ. 보안 통신에서 기존 1 x 2 STLC 기법STLC 호핑 시스템의 부호화 규칙 후보군 설계 방식을 제안하기에 앞서, 보안 통신 측면에서 기존 1 × 2 STLC 시스템을 설명한다[16]. 본 연구에선 1 × 2 STLC 시스템에 두 개 안테나를 갖는 도청자가 존재하는 보안 통신 시나리오를 고려한다. STLC 송신기는 정보 패킷을 부호화하여 사용자에게 전송한다. 각 패킷은 정보 심볼 N개로 구성된 벡터 [TeX:] $$x=\left[x_1 \cdots x_N\right]^T$$이며, 여기서 N은 짝수이다. 송신 안테나로부터 사용자 m째 수신 안테나까지 사용자 채널을 [TeX:] $$h_m$$이라 하며, [TeX:] $$h_m$$은 한 패킷동안 정적이고 패킷 단위로 Rayleigh 분포를 따르며 바뀌는 블록 페이딩 채널이다. 두 개 정보 심볼 [TeX:] $$x_{2 n-1} \text { 과 } x_{2 n}$$에 대한 기존 STLC 부호화 규칙은 다음과 같다[11]:
(1)[TeX:] $$\left[\begin{array}{c} s_{2 n-1}^* \\ s_{2 n} \end{array}\right]=C_1 x=\left[\begin{array}{cc} h_1 & h_2 \\ h_2^* & -h_1^* \end{array}\right]\left[\begin{array}{c} x_{2 n-1} \\ x_{2 n} \end{array}\right] .$$여기서 [TeX:] $$n \in\{1, \ldots, N / 2\}$$이고 [TeX:] $$C_1$$은 STLC 부호화 행렬이다. 최대 송신 전력을 P로 제한하기 위해 STLC 심볼 [TeX:] $$s_{2 n-1} \text { 과 } s_{2 n} \text { 은 } \sqrt{P / \gamma_h}$$로 정규화되며, 연속한 두 심볼 시간 동안 전송된다. 이때, [TeX:] $$\gamma_h=\left|h_1\right|^2+\left|h_2\right|^2$이다. m째 수신 안테나가 시간 n에 수신한 신호를 [TeX:] $$r_{m, n}$$이라 할 때, [TeX:] $$r_{m, n}$$을 다음과 같이 쓸 수 있다. [TeX:] $$(m \in\{1,2\})$$[11]:
(2a)[TeX:] $$r_{m, 2 n-1}=\sqrt{\frac{P}{\gamma_h}} h_m\left(h_1^* x_{2 n-1}^*+h_2^* x_{2 n}^*\right)+z_{m, 2 n-1},$$
(2b)[TeX:] $$r_{m, 2 n}=\sqrt{\frac{P}{\gamma_h}} h_m\left(h_2^* x_{2 n-1}-h_1^* x_{2 n}\right)+z_{m, 2 n} .$$여기서 [TeX:] $$z_{m, n}$$은 가산성 백색 가우스 잡음으로 [TeX:] $$C N\left(0, \sigma^2\right)$$을 따른다. 사용자는 네 개 수신 신호 [TeX:] $$\left\{r_{1,2 n-1}, r_{1,2 n}, r_{2,2 n-1}, r_{2,2 n}\right\}$$의 선형 결합과 등화를 통해 심볼 간 간섭 없이 [TeX:] $$x_{2 n-1} \text { 과 } x_{2 n}$$을 다음과 같이 추정한다[11]:
(3a)[TeX:] $$\frac{\left(r_{1,2 n-1}^*+r_{2,2 n}\right)}{\sqrt{P \gamma_h}}=x_{2 n-1}+\frac{z_{1,2 n-1}^*+z_{2,2 n}}{\sqrt{P \gamma_h}},$$
(3b)[TeX:] $$\frac{\left(r_{2,2 n-1}^*-r_{1,2 n}\right)}{\sqrt{P \gamma_h}}=x_{2 n}+\frac{1}{\sqrt{P \gamma_h}}\left(z_{2,2n-1}^*-z_{1,2 n}\right) .$$(3)을 통해 각 심볼에 대한 사용자 SNR을 다음과 같이 계산할 수 있다[11]:
한편, 도청자 m째 안테나가 시간 n에 수신한 신호 [TeX:] $$y_{m, n}$$은 다음과 같이 쓸 수 있다[16]:
(5a)[TeX:] $$y_{m, 2 n-1}=\sqrt{\frac{P}{\gamma_h}} g_m\left(h_1^* x_{2 n-1}^*+h_2^* x_{2 n}^*\right)+v_{m, 2 n-1},$$
(5b)[TeX:] $$y_{m, 2 n}=\sqrt{\frac{P}{\gamma_h}} g_m\left(h_2^* x_{2 n-1}-h_1^* x_{2 n}\right)+v_{m, 2 n} .$$여기서 [TeX:] $$g_m$$은 송신기로부터 도청자 m째 수신 안테나까지 채널을 의미하며, [TeX:] $$g_{m,n}$$은 가산성 백색 가우스 잡음으로 [TeX:] $$C N\left(0, \sigma^2\right)$$을 따른다. 도청자가 수신 신호 결합 방법과 유효 채널 이득 [TeX:] $$P \gamma_g=P\left(\left|g_1\right|^2+\left|g_2\right|^2\right)$$을 안다고 가정할 때, 도청자는 사용자와 같은 방법으로 정보 심볼을 다음과 같이 추정할 수 있다[16]:
(6a)[TeX:] $$\begin{aligned} & \frac{\left(y_{1,2 n-1}^*+y_{2,2 n}\right)}{\sqrt{P \gamma_g}}=\frac{\left(g_1^* h_1+g_2 h_2^*\right) x_{2 n-1}}{\sqrt{\gamma_g \gamma_h}} \\ & +\frac{\left(g_1^* h_2-g_2 h_1^*\right) x_{2 n}}{\sqrt{\gamma_g \gamma_h}}+\frac{v_{1,2 n-1}^*+v_{2,2 n}}{\sqrt{P \gamma_g}}, \end{aligned}$$
(6b)[TeX:] $$\begin{aligned} & \frac{\left(y_{2,2 n-1}^*-y_{1,2 n}\right)}{\sqrt{P \gamma_g}}=\frac{\left(g_2^* h_1-g_1 h_2^*\right) x_{2 n-1}}{\sqrt{\gamma_g \gamma_h}} \\ & +\frac{\left(g_1 h_1^*+g_2^* h_2\right) x_{2 n}}{\sqrt{\gamma_g \gamma_h}}+\frac{v_{2,2 n-1}^*-v_{1,2 n}}{\sqrt{P \gamma_g}} . \end{aligned}$$사용자가 추정한 정보 심볼과 달리, 도청자가 추정한 정보 심볼에선 사용자 채널 [TeX:] $$h_m$$과 도청자 채널 [TeX:] $$g_m$$의 차이로 인해 심볼 간 간섭이 존재하는 것을 확인할 수 있다. 따라서 기존 연구[7]에서 보인 바와 같이, 사용자와 도청자 채널이 서로 독립인 경우, 기존 STLC 시스템은 높은 보안 성능을 갖는다. 하지만 사용자와 도청자 채널 사이 상관도가 높은 경우, 도청자는 정보 심볼을 성공적으로 복호화할 수 있다. 도청자 채널 [TeX:] $$g_m$$이 사용자 채널 [TeX:] $$h_m$$과 상관 계수 ρ를 갖는다면, [TeX:] $$g_m=\sqrt{\rho^2} h_m+\sqrt{1-\rho^2} f_m$$이다. 여기서 [TeX:] $$0 \leqq \rho \leqq 1 \text { 이고, } f_m \text { 은 }$$ CN(0,1)을 따르며 [TeX:] $$h_m$$과 독립이다. [TeX:] $$\rho=0$$은 도청자와 사용자 채널이 서로 독립인 경우를 의미하며, [TeX:] $$\rho=1$$은 도청자와 사용자 채널이 같은 경우를 의미한다. 채널 상관 계수를 고려할 때, 도청자가 추정한 정보 심볼을 다음과 같이 바꾸어 쓸 수 있다[16]:
(7a)[TeX:] $$\begin{aligned} (6 \mathrm{a})= & \left\langle\rho \sqrt{\frac{\gamma_h}{\gamma_g}}+\sqrt{\frac{1-\rho^2}{\gamma_g \gamma_h}}\left(f_1^* h_1+f_2 h_2^*\right)\right\rangle x_{2 n-1} \\ & +\sqrt{\frac{1-\rho^2}{\gamma_g \gamma_h}}\left(f_1^* h_2+f_2 h_1^*\right) x_{2 n} \\ & +\frac{v_{1,2 n-1}^*+v_{2,2 n}}{\sqrt{P \gamma_g}}, \end{aligned}$$
(7b)[TeX:] $$\begin{aligned} (6 \mathrm{a})= & \left\langle\rho \sqrt{\frac{\gamma_h}{\gamma_g}}+\sqrt{\frac{1-\rho^2}{\gamma_g \gamma_h}}\left(f_1^* h_1+f_2 h_2^*\right)\right\rangle x_{2 n-1} \\ & +\sqrt{\frac{1-\rho^2}{\gamma_g \gamma_h}}\left(f_1^* h_2+f_2 h_1^*\right) x_{2 n} \\ & +\frac{v_{1,2 n-1}^*+v_{2,2 n}}{\sqrt{P \gamma_g}}, \end{aligned}$$(7)을 통해, ρ가 증가할수록 심볼 간 간섭이 감소하여 [TeX:] $$\rho=1$$일 때, 도청자가 추정한 심볼이 사용자가 추정한 심볼과 같음을 알 수 있다. 도청자가 유효 채널 이득(화살 괄호 내부)를 아는 최악의 상황을 가정할 때, 도청자는 사용자와 비슷하거나 같은 통신 성능에 도달할 수 있다. 최악의 상황에 달성할 수 있는 도청자 SNR 상한은 (7a)로부터 다음과 같이 유도할 수 있다[16]:
(8)[TeX:] $$\operatorname{SNR}_1(\rho)=\frac{P\left|\rho \gamma_h+\sqrt{1-\rho^2}\left(f_1^* h_1+f_2 h_2^*\right)\right|^2}{P\left(1-\rho^2\right)\left|f_1^* h_2-f_2 h_1^*\right|^2+2 \gamma_h \sigma^2} .$$(8)을 통해, [TeX:] $$\rho=1$$에서 도청자 SNR 상한은 사용자 SNR과 같음을 확인할 수 있다. Ⅲ. STLC 호핑 기법 부호화 규칙 후보군 설계본 장에선 사용자와 도청자 채널이 높은 상관도를 갖더라도 우수한 보안 성능을 제공하는 STLC 호핑 기법을 소개하고[16], STLC 호핑 시스템의 보안 성능을 높이기 위한 부호화 규칙 후보군을 설계한다. STLC 호핑 시스템 송신기는 두 심볼마다 부호화 규칙 후보군에서 무작위로 부호화 규칙을 선택하여 STLC 심볼을 부호화하고 전송한다. 수신기 측 복호화 규칙은 송신기가 무작위로 선택한 부호화 규칙에 따라 유일하게 결정되므로, 부호화 규칙을 알지못하는 도청자는 잘못된 복호화를 수행하여 수신 SNR 성능이 열화된다. 이때, 높은 보안 성능을 갖는 부호화 규칙을 일부 선정하여 최적 부호화 규칙 후보군을 설계할 수 있다. 3.1 다중 부호화 규칙을 활용한 STLC 호핑 기법기존 STLC 논문[11, Table. 4]을 참조하여 본 논문에서 고려하는 전체 STLC 부호화 규칙을 표 1에서 소개하고 각 부호화 규칙에 따른 복호화 규칙을 표 2에서 정리한다. 부호화 행렬은 채널 정보로 형성한 직교 행렬이며, STLC 부호화 규칙은 부호화 행렬과 부호화 type의 조합으로 결정된다. 부호화 행렬을 [TeX:] $$C_k$$라 할 때, [TeX:] $$C_1, C_2, C_3, C_4$$는 참조한 논문[11, Table. 4]에 기술된 네 개 부호화 행렬이며, 본 연구에선 [TeX:] $$C_1, C_2, C_3, C_4$$의 각 첫째 열과 둘째 열을 뒤바꾸어 네 개 부호화 행렬 [TeX:] $$C_5, C_6, C_7, C_8$$을 추가한다. (즉, [TeX:] $$k \in\{1,2, \ldots, 8\}$$). 예를 들어, 기존 부호화 행렬 [TeX:] $$C_1=\left[\begin{array}{cc} h_1 & h_2 \\ h_2^* & -h_1^* \end{array}\right]$$의 첫째 열과 둘째 열을 바꾼 행렬 [TeX:] $$C_5=\left[\begin{array}{cc} h_2 & h_1 \\ -h_1^* & h_2^* \end{array}\right]$$을 추가한다. 또한, 도청자가 성공적으로 복호화할 수 있는 확률을 줄이기 위하여, 복호화 규칙이 같은 type이 없도록 기존 STLC 논문[11, Table. 4]에 기술된 16 개 type 중 여덟 개 type을 제외한다([TeX:] $$l \in\{1,2, \ldots, 8\}$$). 예를 들어, 송신기가 type, [TeX:] $$\left[\begin{array}{c} s_{2 n-1} \\ s_{2 n}^* \end{array}\right]=C_k^*\left[\begin{array}{c} x_{2 n-1}^* \\ x_{2 n}^* \end{array}\right]$$으로 부호화한다면, 도청자는 Type 1에 해당하는 복호화 규칙을 사용하여 정보 심볼을 복호화할 수 있으므로 해당 type을 제외한다. 송신기는 [TeX:] $$C_k$$와 Type l의 조합으로 64 가지 STLC 부호화 규칙을 사용할 수 있으며, 전체 64 가지 부호화 규칙들로 이루어진 집합을 R로 표기한다. 또한, 부호화 행렬 [TeX:] $$C_k$$와 Type l을 사용한 부호화 규칙 (또는, 복호화 규칙)을 (k,l)로 표기한다. [TeX:] $$a_k, b_k, c_k \text {, 그리고 } d_k$$는 각 정보 심볼을 복호화하기 위한 선형 결합에 사용되는 수신 신호로 [TeX:] $$C_k$$에 따라 결정되며, 수신 신호 선형 결합 방법은 Type l에 따라 결정된다. 전체 64가지 부호화 규칙 중 호핑에 사용하는 부호화 규칙들의 집합을 부호화 규칙 후보군이라고 하며, Q로 표기한다. 부보화 규칙 후보 수는 [TeX:] $$|Q|$$이며, [TeX:] $$|Q|=1$$인 경우 기본 STLC 시스템을 의미한다. 표(Table) 1. 두 개 수신 안테나를 갖는 시스템을 위한 STLC 부호화 규칙 (STLC encoding rule for a system with two receive antennas.)
표(Table) 2. 두 개 수신 안테나를 갖는 시스템을 위한 STLC 복호화 규칙 (STLC decoding rule for a system with two receive antennas.)
STLC 호핑 시스템을 도식화하면 그림 1과 같다. 본 논문에선 Q에 (1,1)을 반드시 포함하며, 도청자는 규칙 (1,1)을 사용해 정보 심볼을 복호화한다고 가정한다. 송신기는 균등한 확률로 Q에서 (k,l)을 추출하여 두 개 정보 심볼 [TeX:] $$x_{2 n-1} \text { 과 } x_{2 n}$$을 부호화하고 전송하며, 규칙 (k,l)은 사용자와 공유된다. 사용자는 규칙 (k,l)을 사용하여 네 개 수신 신호, [TeX:] $$\left\{r_{1,2 n-1}, r_{2,2 n-1}, r_{1,2 n}, r_{2,2 n}\right\}$$을 결합하여 정보 심볼을 복호화한다. 반면, 도청자는 규칙 (1,1)을 사용하여 정보 심볼을 복호화한다. 그림(Fig.) 1. 부호화 규칙 후보군에서 무작위로 부호화 규칙을 선택하는 STLC 호핑 시스템 송수신기 모델 (STLC-hopping system transceiver model where an encoding rule is randomly selected from a candidate group.) 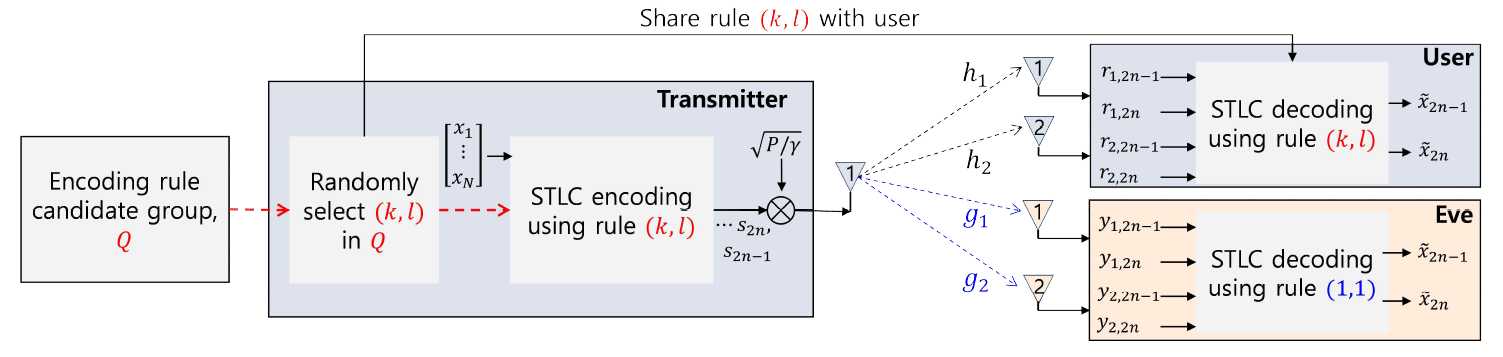 송신기가 규칙 (1,2)를 사용한다면, 사용자 수신 신호 [TeX:] $$r_{m, 2 n-1} \text { 과 } r_{m, 2 n}$$은 다음과 같이 바꾸어 쓸 수 있다[16]:
(9a)[TeX:] $$r_{m, 2 n-1}=\sqrt{\frac{P}{\gamma_h}} h_m\left(h_1^* x_{2 n-1}+h_2^* x_{2 n}^*\right)+z_{m, 2 n-1},$$
(9b)[TeX:] $$r_{m, 2 n}=\sqrt{\frac{P}{\gamma_h}} h_m\left(h_2^* x_{2 n-1}^*-h_1^* x_{2 n}\right)+z_{m, 2 n} .$$사용자는 복호화 규칙 (1,2)를 사용하여 다음과 같이 수신 신호를 결합한다[16]:
(10)을 통해 규칙 (1,2)를 사용하였을 때, 사용자 SNR은 (4)와 같음을 확인할 수 있다. 이와 유사하게, 송신기가 부호화 규칙 (1,2)를 사용 하였을때, 도청자 수신 신호 [TeX:] $$y_{m, 2 n-1} \text { 과 } y_{m, 2 n}$$은 다음과 같이 바꾸어 쓸 수 있다[16]:
(11a)[TeX:] $$y_{m, 2 n-1}=\sqrt{\frac{P}{\gamma_h}} g_m\left(h_1^* x_{2 n-1}+h_2^* x_{2 n}^*\right)+v_{m, 2 n-1},$$
(11b)[TeX:] $$y_{m, 2 n}=\sqrt{\frac{P}{\gamma_h}} g_m\left(h_2^* x_{2 n-1}^*-h_1^* x_{2 n}\right)+v_{m, 2 n} .$$도청자는 복호화 규칙 (1,1)을 사용하며, 도청자가 추정한 정보 심볼 (6a)는 다음과 같이 바꾸어 쓸 수 있다[16]:
(12)[TeX:] $$\begin{aligned} & (6 \mathrm{a})=\left\langle\frac{\rho \gamma_h+\sqrt{1-\rho^2}\left(f_1^* h_1+f_2 h_2^*\right)}{\sqrt{\gamma_g \gamma_h}}\right\rangle x_{2 n-1}^* \\ & +\frac{\sqrt{1-\rho^2}\left(f_1^* h_2-f_2 h_1^*\right)}{\sqrt{\gamma_g \gamma_h}} x_{2 n}+\frac{v_{1,2 n-1}^*+v_{2,2 n}}{\sqrt{P \gamma_g}} . \end{aligned}$$[TeX:] $$\rho=1$$인 경우, 도청자는 정보 심볼의 켤레 복소수를 추정하게 되며, 도청자 SNR 상한은 다음과 같다:
(13)[TeX:] $$\mathrm{SNR}_2(1)=\frac{P \gamma_h}{2 \sigma^2+2 P \gamma_h}\lt \frac{P \gamma_h}{2 \sigma^2}=\mathrm{SNR}_{\mathrm{B}}$$(13)에 대한 유도 과정은 부록을 통해 확인할 수 있으며, 사용자와 도청자 채널이 같은 상황에서도 도청자 SNR이 사용자 SNR 대비 항상 낮음을 알 수 있다. 위와 같은 방식으로 송신기가 부호화 규칙 (k,l)을 사용할 때 얻는 도청자 SNR 상한을 유도할 수 있으며, 총 아홉 가지로 나타나는 도청자 SNR 상한 [TeX:] $$\mathrm{SNR}_i$$를 표 3에 정리하였다 [TeX:] $$(i \in\{1, \ldots, 9\})$$ 표 3을 통해 Case 1을 제외한 여덟 가지 경우에 대해서 [TeX:] $$\rho=1$$일 때, 도청자 SNR 상한이 사용자 SNR 보다 낮음을 확인할 수 있다. 표 4에선 각 부호화 규칙 (k,l)을 사용할 때, [TeX:] $$\tilde{x}_{2 n-1} \text { 와 } \tilde{x}_{2 n}$$에 대해 도청자가 얻는 SNR 상한인 [TeX:] $$\mathrm{oSNR}_{k, l} \text { 과 } \mathrm{eSNR}_{k, l}$$을 정리하였다. 표(Table) 3. STLC 호핑 시스템에서 도청자 SNR 상한 (SNR upper bound of Eve in STLC hopping systems.)
표(Table) 4. 도청자가 복호화 규칙 (1,1)을 사용한다고 가정할 때, 부호화 규칙 (k, l)에 따른 각 심볼에 대한 도청자 SNR 상한 (Eve's SNR upper bound for each symbol according to encoding rule (k, l) when Eve uses decoding rule (1,1).)
3.2 STLC 호핑에 따른 보안 전송률 하한 모델 정의부호화 규칙 (k,l)에 따른 심볼 당 도청자 SNR 상한인 [TeX:] $$\mathrm{oSNR}_{k, l} \text { 과 } \mathrm{eSNR}_{k, l}$$을 통해, 각 심볼 당 SRLB를 다음과 같이 계산할 수 있다[19, 20]:
(14a)[TeX:] $$\begin{aligned} & \mathrm{OSRLB}_{k, l} \\ & =\mathrm{E}\left[\left(\log _2\left(1+\mathrm{SNR}_{\mathrm{B}}\right)-\log _2\left(1+\mathrm{oSNR}_{k, l}\right)\right)^{+}\right], \end{aligned}$$
(14b)[TeX:] $$\begin{aligned} & \mathrm{eSRLB}_{k, l} \\ & =\mathrm{E}\left[\left(\log _2\left(1+\mathrm{SNR}_{\mathrm{B}}\right)-\log _2\left(1+\mathrm{eSNR}_{k, l}\right)\right)^{+}\right] . \end{aligned}$$이때, 기댓값 연산자는 채널에 대한 평균을 의미한다. STLC 시스템은 연속한 두 심볼마다 부호 및 복호화를 수행하므로, 부호화 규칙 (k,l)을 사용할 때 SRLB를 다음과 같이 정의한다:
송신기가 균등한 확률로 부호화 규칙 후보군에서 규칙 (k,l)을 선택하여 사용하므로, STLC 호핑 시스템의 SRLB를 다음과 같이 쓸 수 있다:
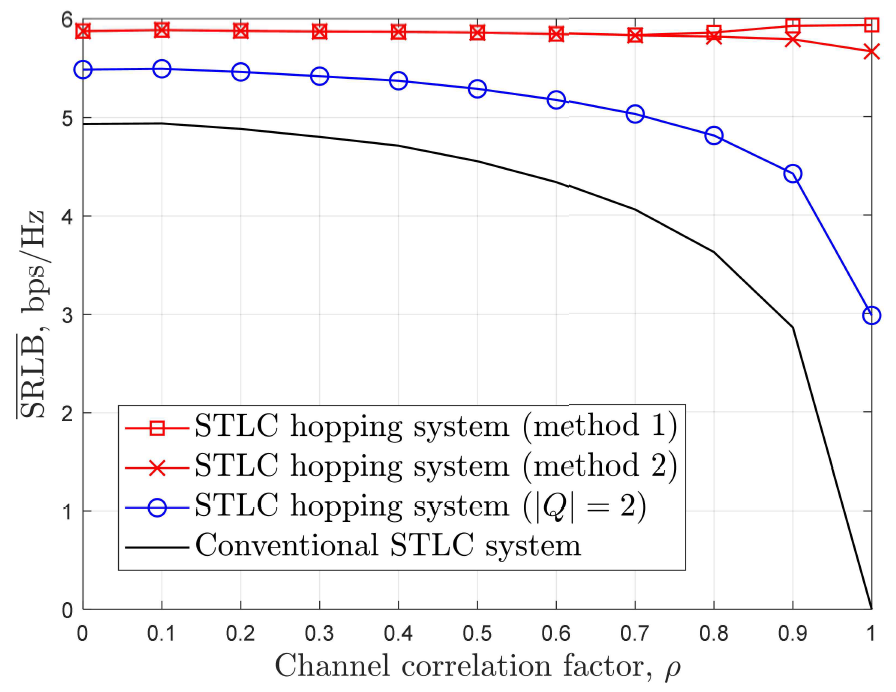
(8)에서 확인할 수 있듯이, [TeX:] $$\rho=1$$에서 [TeX:] $$\mathrm{SNR}_1=\mathrm{SNR}_{\mathrm{B}}$$이므로 기존 STLC 시스템에서 [TeX:] $$\overline{\mathrm{SRLB}}=0$$이다. 반면, STLC 호핑 시스템에서 규칙 (1,1)을 제외한 규칙 (k,l)에 대해서 [TeX:] $$\mathrm{SRLB}_{k, l}\gt 0 \text { 이므로 } \overline{\mathrm{SRLB}}\gt 0$$이다. 3.3 부호화 규칙 후보군 설계본 절에선 STLC 호핑 시스템의 보안 성능을 높이기 위한 부호화규칙 후보군, Q를 설계한다. 표 4와 (15)를 활용하여 [TeX:] $$\mathrm{SRLB}_{k, l}$$을 계산하고, 높은 [TeX:] $$\mathrm{SRLB}_{k, l}$$을 얻는 순으로 (k,l)을 Q에 추가하는 방식으로 최적 Q를 설계할 수 있다. 이때, [TeX:] $$\mathrm{SRLB}_{k, l}$$은 채널 상관 계수 ρ에 따라 달라지므로, 최적 Q는 ρ에 따라 결정된다. 그림 2는 해당 방식을 사용할 때 얻는 [TeX:] $$\overline{\mathrm{SRLB}}$$ 성능이며, 그림 2를 통해 각 ρ에 대한 최적 Q가 존재함을 알 수 있다. 따라서 송신기가 ρ를 알 때, 다음과 같은 방식 1로 최적 Q를 설계한다. 그림(Fig.) 2. 높은 SRLB를 얻는 규칙 순으로 (k,l)을 부호화 규칙 후보군에 추가할 때, STLC 호핑 시스템의 SRLB 성능 [TeX:] $$\left(1 / \sigma^2=20 \mathrm{~dB}, \quad \rho \in\{0,0.8,1\}\right)$$ (STLC hopping system SRLB performance, when (k,l) is added to the encoding rule candidate group in the order of obtaining high SRLB [TeX:] $$\left(1 / \sigma^2=20 \mathrm{~dB}, \quad \rho \in\{0,0.8,1\}\right)$$) 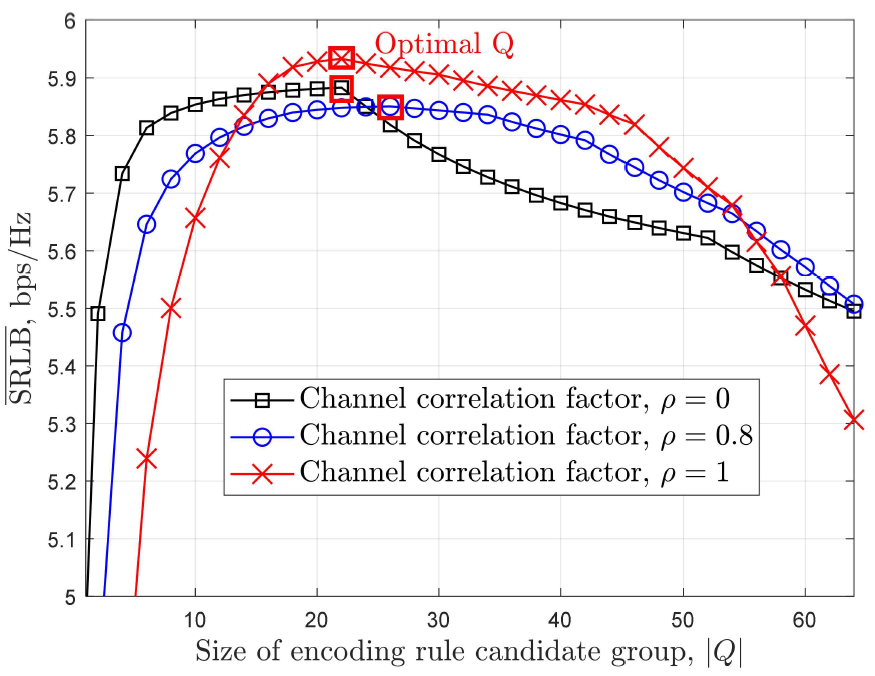 방식 1 (ρ에 대한 정보가 있을 때): [TeX:] $$\overline{\mathrm{SRLB}}$$가 감소할 때까지 높은 [TeX:] $$\mathrm{SRLB}_{k, l}$$을 얻는 순서로 부호화 규칙 (k,l)을 후보군에 추가한다. 방식 1을 통한 부호화 규칙 후보군 설계 과정은 알고리즘 1에서 확인할 수 있다. 하지만 해당 방식은 ρ에 대한 정보를 요구하므로, ρ에 대한 정보가 없을 때 활용할 수 있는 다음과 같은 부호화 규칙 후보군 설계 방식 2를 제안한다. 방식 2 (ρ에 대한 정보가 없을 때): 부호화 규칙 (1,1), (1,4), (1,5), (1,6), (1,7), (1,8), (2,4), (2,8), (3,2), (3,4), (3,7), (3,8), (4,4), (4,8), (5,4), (5,8), (6,4), (6,8), (7,4), (7,8), (8,4), (8,8)로 부호화 규칙 후보군을 설계한다. 방식 2에서 사용하는 부호화 규칙은 [TeX:] $$1 / \sigma^2=20 \mathrm{~dB}$$일 때, 전 ρ 구간에서 [TeX:] $$\mathrm{SRLB}_{k, l}$$이 5.5 bps/Hz 이상인 부호화 규칙들이다. Ⅳ. 모의실험 결과본 장에선 모의실험을 통해 설계한 부호화 규칙 후보군을 사용하는 STLC 호핑 시스템의 성능을 보인다. 그림 3은 [TeX:] $$1 / \sigma^2=20 \mathrm{~dB}$$일 때 채널 상관 계수 ρ에 따른 STLC 호핑 시스템 SRLB 비교 결과이며, 기존 STLC 기법과 부호화 규칙 후보군으로 규칙 (1,1)과 (1,5)를 사용한 STLC 호핑 기법 (즉, [TeX:] $$|Q|=2$$)를 함께 비교한다. 그림 3을 통해, STLC 호핑 기법이기존 STLC 기법 대비 우수한 보안 성능을 제공함을 확인할 수 있다. 특히, [TeX:] $$\rho=1$$에서 기존 STLC 시스템은 SRLB가 0인 반면, STLC 호핑 기법은 [TeX:] $$\rho=1$$에서 높은 SRLB를 제공한다. 제안한 부호화 규칙 후보군을 사용한 STLC 호핑 시스템은 [TeX:] $$|Q|=2$$인 STLC 호핑 시스템과 비교하여 전 구간에서 우수한 성능을 보였으며, 방식 1을 사용할 때 최적 SRLB 성능을 얻었다. 방식 1, 최적 STLC 호핑 기법은 [TeX:] $$\rho \geq 0.7$$에서 ρ가 증가함에 따라 SRLB가 증가하였으며, [TeX:] $$\rho=1$$에서 [TeX:] $$\rho=0$$일 때보다 높은 SRLB를 얻었다. 방식 2를 사용한 STLC 호핑 기법은 [TeX:] $$\rho \lt 0.7$$에서 최적 STLC 호핑 기법에 준하는 성능을 보였으며, [TeX:] $$\rho \geq 0.7$$에서 최적 STLC 호핑 기법 대비 성능이 떨어지기 시작하여 [TeX:] $$\rho=1$$에서 4.5% 성능 저하가 발생했다. 이는 방식 2로 설계한 부호화 규칙 후보군에 [TeX:] $$\rho=1$$에서 가장 높은 SRLB를 얻는 부호화 규칙을 포함하지 않아 생기는 성능 열화이다. Ⅴ. 결 론본 논문에선 STLC 호핑 시스템 보안 성능을 최대화하기 위한 부호화 규칙 후보군을 설계하였다. STLC 호핑 시스템 송신기는 두 심볼마다 부호화 규칙을 무작위로 선택하여 도청자가 올바른 복호화 규칙을 알지 못하도록 하고, 이에 따라 도청자 수신 SNR 성능을 열화시킨다. 이때, 높은 보안 성능을 얻는 일부 규칙으로 부호화 규칙 후보군을 설계하여 보안 성능을 최대화 할 수 있다. 채널 상관 계수 ρ에 대한 정보가 있는 경우, STLC 호핑 시스템 SRLB가 감소할 때까지 높은 SRLB를 얻는 부호화 규칙을 후보군에 추가한다. ρ에 대한 정보가 없는 경우, [TeX:] $$1 / \sigma^2=20 \mathrm{~dB}$$일 때, SRLB가 5.5 bps/Hz 이상인 부호화 규칙들로 후보군을 구성한다. 모의실험 결과, 제안한 부호화 규칙 후보군을 사용한 STLC 호핑 시스템이 기존 방식 대비 높은 보안 성능을 제공함을 확인하였다. 특히, 송신기가 ρ에 대한 정보를 알 때, 최적 보안 성능을 달성하였으며, ρ에 대한 정보가 없을 때는 설계한 STLC 호핑 기법이 최적 STLC 호핑 기법의 95.5%에 달하는 보안 성능을 얻었다. 부 록송신기가 STLC 부호화 규칙 (1,2)를 사용하고 도청자는 복호화 규칙 (1,1)을 사용할 때, 심볼 [TeX:] $$\tilde{x}_{2 n-1}$$에 대한 도청자 SNR 상한은 다음의 과정으로 유도할 수 있다. 우선 (12)를 다음과 같이 전개한다:
(17)[TeX:] $$\begin{aligned} (12) & =\left(\frac{\rho \gamma_{h+} \sqrt{1-\rho^2}\left(f_1^* h_1+f_2 h_2^*\right)}{\sqrt{\gamma_g \gamma_h}}\right) \\ & \times\left(x_{2 n-1}-2 j \mathfrak{I}\left(x_{2 n-1}\right)\right) \\ & +\frac{\sqrt{1-\rho^2}\left(f_1^* h_2-f_2 h_1^*\right)}{\sqrt{\gamma_g \gamma_h}} x_{2 n}+\frac{v_{1,2 n-1}^*+v_{2,2 n}}{\sqrt{P \gamma_g}} \\ & =S+N . \end{aligned}$$이때, S와 N은 다음과 같다:
(18)[TeX:] $$S=\frac{\rho \gamma_h+\sqrt{1-\rho^2}\left(f_1^* h_1+f_2 h_2^*\right)}{\sqrt{\gamma_g \gamma_h}} x_{2 n-1},$$
(19)[TeX:] $$\begin{aligned} & N=-2 j \frac{\rho \gamma_h+\sqrt{1-\rho^2}\left(f_1^* h_1+f_2 h_2^*\right)}{\sqrt{\gamma_g \gamma_h}} \Im\left(x_{2 n-1}\right) \\ & +\frac{\sqrt{1-\rho^2}\left(f_1^* h_2-f_2 h_1^*\right)}{\sqrt{\gamma_g \gamma_h}} x_{2 n}+\frac{v_{1,2 n-1}^*+v_{2,2 n}}{\sqrt{P \gamma_g}} . \end{aligned}$$여기서 도청자 SNR 상한은 다음과 같다:
(20)[TeX:] $$\operatorname{SNR}_2(\rho)=\frac{\mathrm{E}\left[|S|^2\right]}{\mathrm{E}\left[|N|^2\right]} .$$[TeX:] $$\mathrm{E}\left[|N|^2\right]$$은 쪽 아래에 위치한 (21a)와 같이 쓸 수 있다. 심볼 [TeX:] $$x_{2 n-1} \text { 과 } x_{2 n}$$은 독립이며, [TeX:] $$\mathrm{E}\left[|x|^2\right]=1,\mathrm{E}\left[|\mathfrak{I}(x)|^2\right]=1 / 2, \mathrm{E}\left[\mathfrak{I}\left(x_{2 n-1}\right) x_{2 n}^*\right]=0$$이므로 (21a)는 (21b)와 같다. 따라서, 송신기가 부호화 규칙 (1,2)를 사용하고 도청자는 복호화 규칙 (1,1)을 사용할 때, [TeX:] $$\tilde{x}_{2 n-1}$$ 신호에 대한 도청자 SNR 상한은 표 3 Case 2가 된다. 여기서 도청자 SNR 상한에 [TeX:] $$\rho=1$$을 대입하면 (13)을 얻을 수 있다.
(21a)[TeX:] $$\mathrm{E}\left[|N|^2\right]=\frac{1}{\gamma_h \gamma_g} \mathrm{E}\left[\left|-2 j\left(\rho \gamma_h+\sqrt{1-\rho^2}\left(f_1^* h_1+f_2 h_2^*\right)\right) \mathfrak{I}\left(x_{2 n-1}\right)+\sqrt{1-\rho^2}\left(f_1^* h_2-f_2 h_1^*\right) x_{2 n}\right|^2\right]+\frac{2 \sigma^2}{P \gamma_g}$$
BiographyBiographyBiography정 진 곤 (Jingon Joung)2001년 2월 : 연세대학교 전파 공학과 졸업 2003년 2월 : KAIST 전자전산 학과 석사 2007년 2월 : KAIST 전자전산 학과 박사 2007년 3월~2008년 8월 : KAIST, 박사후연구원 2007년 8월~2008년 8월 : ㈜ 루미콤, 위촉연구원 2008년 9월~2009년 9월 : UCLA, 박사후연구원 2009년 10월~2016년 2월 : I2R, Singapore, 연구원 2016년 3월~현재 : 중앙대학교 전자전기공학부 교수 <관심분야> 무선통신, 통신 신호처리, 기계학습 [ORCID:0000-0002-9551-1123] References
|
StatisticsCite this articleIEEE StyleT. Choi, J. Kim, J. Joung, "Encoding-Rule-Candidate Group Design for Security Rate Enhancement of Space-Time Line Code Hopping Systems," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 7, pp. 1058-1068, 2025. DOI: 10.7840/kics.2025.50.7.1058.
ACM Style Taehee Choi, Jaehong Kim, and Jingon Joung. 2025. Encoding-Rule-Candidate Group Design for Security Rate Enhancement of Space-Time Line Code Hopping Systems. The Journal of Korean Institute of Communications and Information Sciences, 50, 7, (2025), 1058-1068. DOI: 10.7840/kics.2025.50.7.1058.
KICS Style Taehee Choi, Jaehong Kim, Jingon Joung, "Encoding-Rule-Candidate Group Design for Security Rate Enhancement of Space-Time Line Code Hopping Systems," The Journal of Korean Institute of Communications and Information Sciences, vol. 50, no. 7, pp. 1058-1068, 7. 2025. (https://doi.org/10.7840/kics.2025.50.7.1058)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||